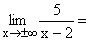
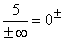
Gf hat die waagrechte Asymptote y=0 mit Annäherung von unten und oben her.
| 1. | 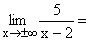 |
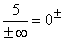 |
5 geteilt durch eine sehr große positive(negative) Zahl ergibt eine sehr kleine positive(negative) Zahl, also ±0 .
Gf hat die waagrechte Asymptote y=0 mit Annäherung von unten und oben her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 2. | 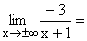 |
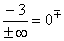 |
-3 geteilt durch eine sehr große positive(negative) Zahl ergibt eine sehr kleine positive(negative) Zahl, also ±0 .
Gf hat die waagrechte Asymptote y=0 mit Annäherung von unten und oben her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 3. | 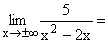 |
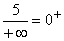 |
Im Nenner spielt nur x2 für große Zahlen eine Rolle. Durch das Quadrat werden auch negative Zahlen positiv. 5 geteilt durch eine sehr große positive Zahl ergibt eine sehr kleine positive Zahl, also 0+ . Gf hat die waagrechte Asymptote y=0 mit Annäherung nur von oben her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 4. | 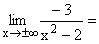 |
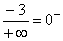 |
Durch das Quadrat im Nenner werden auch negative Zahlen positiv. -3 geteilt durch eine sehr große positive Zahl ergibt eine sehr kleine negative Zahl, also 0¯ . Gf hat die waagrechte Asymptote y=0 mit Annäherung nur von unten her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 1. | 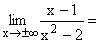 |
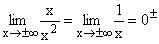 |
Im Zähler werden alle Potenzen unter x, im Nenner alle unter x2 sowie alle Konstanten weggelassen und dann x gekürzt. 1 geteilt durch eine sehr große positive(negative) Zahl ergibt ±0 . Gf hat die waagrechte Asymptote y=0 mit Annäherung von unten und oben her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 2. | 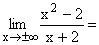 |
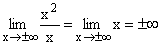 |
Im Zähler werden alle Potenzen unter x2, im Nenner alle unter x sowie alle Konstanten weggelassen und dann x gekürzt. Als Grenzwert ergibt sich ganz klar ±¥ Gf hat eine schräge Asymptote , da der Zählergrad um 1 höher ist, als der Nennergrad. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 3. | 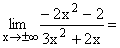 |
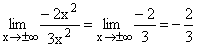 |
Im Zähler und im Nenner werden alle Potenzen unter x2 sowie alle Konstanten weggelassen und dann x2 gekürzt. Als Grenzwert ergibt sich ganz klar -2/3 . Gf hat die waagrechte Asymptote y=-2/3 . |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 4. | 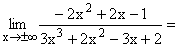 |
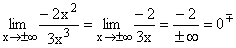 |
Im Zähler werden alle Potenzen unter x2, im Nenner alle unter x3 sowie alle Konstanten weggelassen und dann x2 gekürzt. -2 geteilt durch eine sehr große positive(negative) Zahl ergibt eine sehr kleine negative(positive) Zahl, also 0 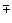 . .
Gf hat die waagrechte Asymptote y=0 mit Annäherung von unten und oben her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 1. | 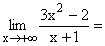 |
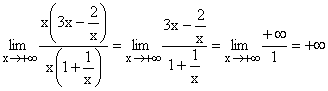 |
Nach Ausklammern von x im Zähler und Nenner und Kürzen,
geht der Nenner gegen 1, der Zähler gegen +¥ , da die Terme 2/x und 1/x gegen Null gehen.
Gf hat eine schräge Asymptote , da der Zählergrad um 1 höher ist, als der Nennergrad. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 2. | 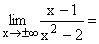 |
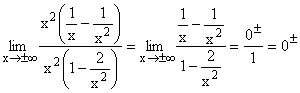 |
Nach Ausklammern von x2 im Zähler und Nenner und Kürzen,
geht der Zähler gegen 0, der Nenner gegen 1 , da alle Terme mit 1/x2 und 1/x gegen Null gehen. Im Zähler bestimmt nur der Term 1/x das Vorzeichen der Null. Gf hat die waagrechte Asymptote y=0 mit Annäherung von unten und oben her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 3. | 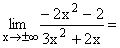 |
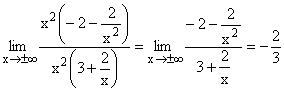 |
Nach Ausklammern von x2 im Zähler und Nenner und Kürzen,
geht der Zähler gegen -2, der Nenner gegen 3 , da die Terme 2/x2 und 2/x gegen Null gehen.
Gf hat die waagrechte Asymptote y=-2/3 . |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 4. | 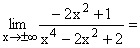 |
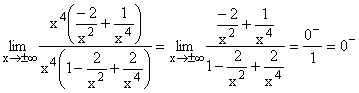 |
Nach Ausklammern von x4 im Zähler und Nenner und Kürzen,
geht der Zähler gegen 0, der Nenner gegen 1 , da alle Terme mit 1/x2 und 1/x4 gegen Null gehen. Im Zähler bestimmt nur der Term -2/x2 das Vorzeichen der Null und zwar Minus . Gf hat die waagrechte Asymptote y=0 mit Annäherung nur von unten her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 1. | 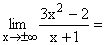 |
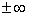 |
Der Zählergrad z=2 ist größer als der Nennergrad n=1, deshalb als Ergebnis ¥ . Der Zähler ist für große positive(negative) Zahlen immer positiv, der Nenner wechselt das Vorzeichen, deshalb auch Vorzeichenwechsel beim Ergebnis. Gf hat eine schräge Asymptote , da der Zählergrad um 1 höher ist, als der Nennergrad. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 2. | 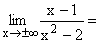 |
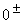 |
Der Zählergrad z=1 ist kleiner als der Nennergrad n=2, deshalb als Ergebnis 0. Der Nenner ist für große positive(negative) Zahlen immer positiv, der Zähler wechselt das Vorzeichen, deshalb auch Vorzeichenwechsel beim Ergebnis. Gf hat die waagrechte Asymptote y=0 mit Annäherung von unten und oben her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 3. | 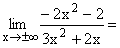 |
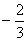 |
Der Zählergrad z = 2 ist gleich dem Nennergrad n = 2 . Deshalb als Ergebnis: az/an = - 2/3 . Gf hat die waagrechte Asymptote y=-2/3 . |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 4. | 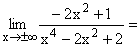 |
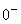 |
Der Zählergrad z=2 ist kleiner als der Nennergrad n=4, deshalb als Ergebnis 0. Der Nenner ist für große positive(negative) Zahlen immer positiv, der Zähler immer negativ wegen -2x2 , deshalb Null Minus. Gf hat die waagrechte Asymptote y=0 mit Annäherung nur von unten her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 5. | 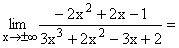 |
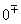 |
Der Zählergrad z=2 ist kleiner als der Nennergrad n=3, deshalb als Ergebnis 0. Der Zähler ist für große positive(negative) Zahlen immer negativ wegen -2x2 , der Nenner wechselt das Vorzeichen, deshalb Null Minus/Plus. Gf hat die waagrechte Asymptote y=0 mit Annäherung von unten und oben her. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 1. | 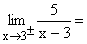 |
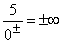 |
5 geteilt durch eine sehr kleine positive(negative) Zahl ergibt eine sehr große positive(negative) Zahl, also ±¥ . Gf hat bei x=3 die senkrechte Asymptote x=5 mit Vorzeichensprung. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 2. | 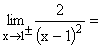 |
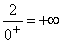 |
2 geteilt durch eine sehr kleine positive Zahl ergibt eine sehr große positive Zahl, also ±¥ . Gf hat bei x=1 die senkrechte Asymptote x=1 ohne Vorzeichensprung. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 3. | 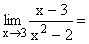 |
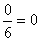 |
Dieser Grenzwert hat eigentlich keine wichtige Bedeutung. Er sagt nur aus, dass man sich dem Punkt (3/0) von beiden Seiten her nähert. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 4. | 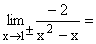 |
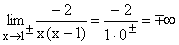 |
-2 geteilt durch eine sehr kleine positive(negative) Zahl ergibt eine sehr große negative(positive) Zahl, also -/+¥ . Das Faktorisieren des Nenners macht die Entscheidung über die Art der Annäherung (links-rechts) einfacher. Gf hat bei x=1 die senkrechte Asymptote x=1 mit Vorzeichensprung. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 5. | 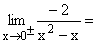 |
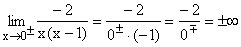 |
-2 geteilt durch eine sehr kleine negative(positive) Zahl ergibt eine sehr große positive(negative) Zahl, also ±¥ . Das Faktorisieren des Nenners macht die Entscheidung über die Art der Annäherung (links-rechts) einfacher. Gf hat bei x=0 die senkrechte Asymptote x=0 mit Vorzeichensprung. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 1. | 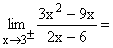 |
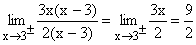 |
Nach Faktorisieren von Zähler und Nenner und Kürzen von x-3 verschwindet die gemeinsame Nullstelle 3 und es ergibt sich der klare Grenzwert 9/2. Die Stelle x = 3 ist eine stetig behebbare Definitionslücke von f(x). |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 2. | 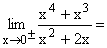 |
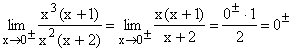 |
Nach Faktorisieren von Zähler und Nenner und Kürzen von x2 bleibt die gemeinsame Nullstelle 0 im Zähler stehen und es ergibt sich der klare Grenzwert 0. Die Stelle x = 0 ist eine stetig behebbare Definitionslücke von f(x). |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 3. | 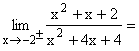 |
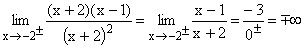 |
Nach Faktorisieren von Zähler und Nenner und Kürzen von x+2 bleibt die gemeinsame Nullstelle -2 im Nenner stehen und es ergibt sich der klare Grenzwert -/+¥ . Gf hat bei x=-2 die senkrechte Asymptote x=-2 mit Vorzeichensprung. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 4. | 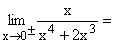 |
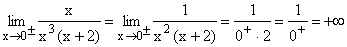 |
Nach Faktorisieren von Zähler und Nenner und Kürzen von x bleibt die gemeinsame Nullstelle 0 doppelt im Nenner stehen und es ergibt sich der klare Grenzwert +¥ .
Gf hat bei x=0 die senkrechte Asymptote x=0 ohne Vorzeichensprung. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 1. | 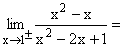 |
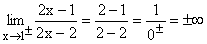 |
Nach einmaligem getrennten Ableiten von Zähler und Nenner kann 1 eingesetzt werden und es ergibt sich der klare Grenzwert Zahl/0 = ∞. Gf hat bei x=1 die senkrechte Asymptote x=1 mit Vorzeichensprung. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 2. | 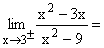 |
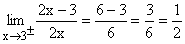 |
Nach einmaligem getrennten Ableiten von Zähler und Nenner kann 3 eingesetzt werden und es ergibt sich der klare Grenzwert 1/2. Die Stelle x = 3 ist eine stetig behebbare Definitionslücke von f(x). |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 3. | 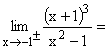 |
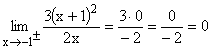 |
Nach einmaligem getrennten Ableiten von Zähler und Nenner kann -1 eingesetzt werden und es ergibt sich der klare Grenzwert 0/Zahl = 0 . Die Stelle x = -1 ist eine stetig behebbare Definitionslücke von f(x). |
| Lösung zeigen - | verbergen | Kapiert? Nein! |
| 4. | 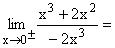 |
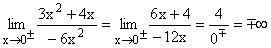 |
Erst nach zweimaligem getrennten Ableiten von Zähler und Nenner kann 0 eingesetzt werden und es ergibt sich der klare Grenzwert Zahl/0 = ∞ . Gf hat bei x=0 die senkrechte Asymptote x=0 mit Vorzeichensprung. |
| Lösung zeigen - | verbergen | Kapiert? Nein! |