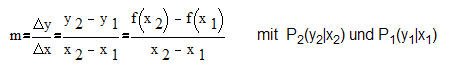
Navigation: Seite zurück und Seite vor

Klären wir nun die Fragen:

1.) Mit welcher Geschwindigung prallt das Objekt auf die Erde (Aufprallgeschwindigkeit)?

Antwort: Die Aufprallgeschwindigkeit ist somit die Momentangeschwindigkeit. Welchen Wert diese erreicht, klären wir unten.

2.) Mit welcher durchschnittlichen Geschwindigkeit legt das Objekt die Höhe von 1000m zurück?

Antwort: Die Durchschnittsgeschwindigkeit ist die konstante Geschwindigkeit mit der das Objekt in der gleichen Zeit die gleiche Strecke zurücklegt. Hier wird in Δt=14,27s die Strecke Δs=1000m zurückgelegt. v_D = 1000m/14,27s => v_D = 70,08m/s.

3.) Wie sind diese Geschwindigkeiten in diesem s-t-Diagramm geometrisch erkennbar?

Antwort: Die Durschnittsgeschwindigkeit wird mit der Steigung der Geraden (grün) geometrische erfasst. Bei den linearen Funktionen haben wir kennen gelernt:

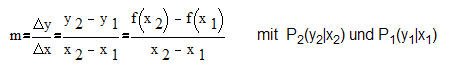
Versuchen wir nun mit den zusammengestellten Informationen den Wert der Momentangeschwindigkeit zu klären.

1. Ansatz: Wir haben erfahren, dass die Fallgeschwindigkeit in jeder Sekunde um 9,81m/s ansteigt. Nach 14,27s also: v = 14,27•9,81m/s also: v = 140m/s.

2. Ansatz: Zu Beginn ist die Geschschwindigkeit v₀= 0 m/s. Im Durchschnitt hatten wir v_D = 70,08m/s ermittelt. Für die Berechnung des Mittelwertes gilt:
---------------
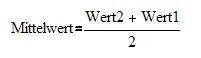
Also:
-----------

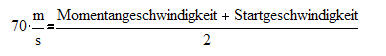
Auch hier erhalten wir die Momentangeschwindigkeit von v= 140m/s.

Wie ist dieser Wert geometrisch zu bewerten. Das Applet gibt uns nun die Möglichkeit den grünen Punkt in den roten Punkt zu verschieben.

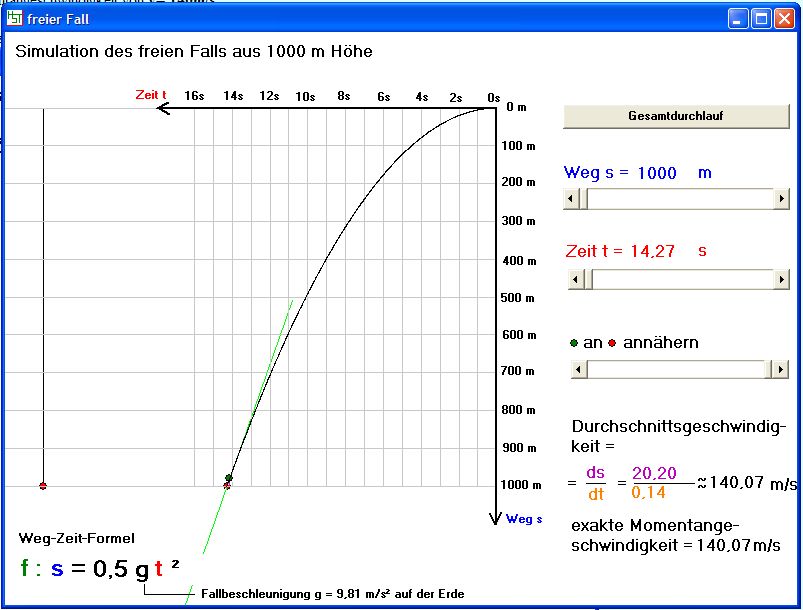
Wir erkennen, dass auch diese Geschwindigkeiten im s-t-Diagramm mit der Steilheit eine geraden verknüpft ist. Wenn die beiden Punkte "verschmelzen", haben wir eine Gerade, die die Kurve in nur einem Punkt berührt.

Vergleichen wir die beiden untersuchten Fälle:

Bei der Frage nach der Durchnittsgeschwindigkeit haben wir das Ergebnis über die Steilheit der grünen Kennlinie erhalten.
Diese Kennlinie schneidet den aufgezeichneten Verlauf in zwei Punkten. Eine solche Gerade wird in der Geometrie mit Sekante bezeichnet.

Bei der Frage der Momentangeschwindigkeit haben wir das Ergebnis über die Steilheit einer Geraden ermittelt, die den aufgezeichneten Verlauf in einem Punkt berührte. Eine solche Gerade wird in der Geometrie mit Tangente bezeichnet.

In beiden Fällen ist die Beantwortung der gestellten Fragen immer mit der Steigung verbunden.
Diese Grundfragestellung ist das Kernproblem der Differentialrechnung.

Bevor weitere Überlegungen dazu angestellt werden, muss zunächst geklärt werden, wie sinnvoller Weise bei einer "gekrümmten Linie" die Steigung interpretiert wird. In der Mathematik wurde definiert:

In unserem Einstiegbeispiel war die "Kurve" eine Fallparabel. Mit dem Durchschnittswert g ≈ 10m/s² erhalten die mathematische Zuordnung: y=f(x)= 5•x² (Beachte: oben ist der 1. Quadrat dargestellt). Hier liegt eine nach unten geöffnete und gestreckte Parabel vor.

Wichtig: Im Rahmen der Differentialrechnung geht es immer wieder um Tangenten und Tangentensteigungen. Tangenten sind Geraden und somit die Graphen linearer Funktionen. Wiederholen Sie daher dringend das Thema "Lineare Funktionen". Alle dort erarbeiteten Grundaufgaben sind auch jetzt wieder umzusetzen. (Wiederholung bei Brinkmann-DU, Whlg1, Whlg2!!!!)

Für die weiteren Überlegungen greifen zur Vereinfachung eine nach oben geöffnete und mit dem Faktor 2 gestreckte Parabel auf und lösen eine vergleichbare Problematik im 1. Quadraten des Koordinatensystems.

weiter zur 3. Seite