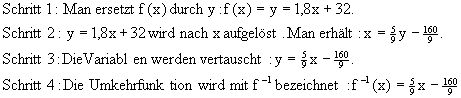
| Station 20 | Lösungen | J |
Umkehrfunktionen
Aufgabe 1
a) Es sind zwei Punkte der Funktion bekannt: der Gefrierpunkt (0|32) und der Siedepunkt (100| 212), wobei die x-Koordinate die Temperatur in Grad Celsius und die y-Koordinate die Temperatur in Grad Fahrenheit angibt. Durch Einsetzen in die Zwei-Punkte-Form der Geradengleichung erhält man die Funktionsgleichung f(x)=1,8x+32.
b)
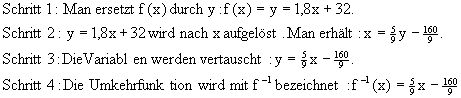
Die Graphen der Funktionen verlaufen wie folgt: (Die Umkehrfunktion wird hier u genannt, w ist die Winkelhalbierende.)
.
Vergleich der beiden Funktionsgraphen:
Wenn man eine Winkelhalbierende einzeichnet, sieht man, dass der Graph der Umkehrfunktion durch Spiegelung des ursprünglichen Graphen an der Winkelhalbierenden entsteht.
c) Umkehrfunktionen
Geometrisch erhält man den Graphen der Umkehrfunktion durch Spiegelung des Graphen der Funktion an der Winkelhalbierenden w mit w(x)=x.
Eine Funktion ist nur dann umkehrbar, wenn jede Parallele zur x-Achse den Graphen der Funktion höchstens einmal schneidet.
| zurück |