Lösung mit einer Funktion:

x = Anzahl der Preissenkungen um je 50 Euro ;   y = Einnahmen pro Tag in Euro

y = (400 - 50x) (1050 + 300x) ergibt ausmultipliziert y = -15000x² + 67500x + 420000

Die Gleichung beschreibt eine quadratische Funktion. Ihr Graph ist eine nach unten geöffnete Parabel. Die gesuchten Werte entsprechen daher genau dem Scheitelpunkt. Der Scheitelpunkt lässt sich durch Umformen in die Scheitelpunktform bestimmen:

y = -15000(x - 2,25)² +  495937,5     also S(2,25/ 495937,5)

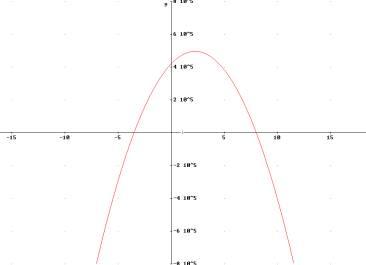
Eine weiterer Lösungsweg geht über das Lösen von quadratischen Gleichungen. Wenn eine quadratische Funktion zwei Nullstellen aufweist, liegt der Scheitelpunkt in der Mitte der beiden Nullstellen. Die beiden Nullstellen liegen bei x = -3,5 und x = 8.