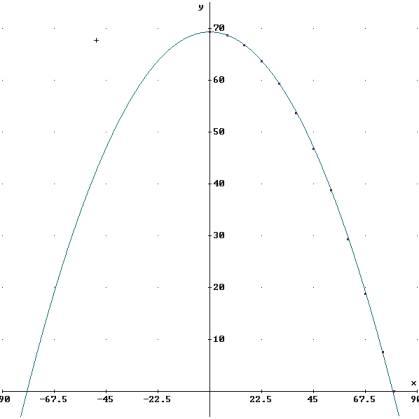
a) Da der Scheitelpunkt (0/69,3) bekannt ist, ergibt sich der Ansatz f(x) = ax² + 69,3.

Je nachdem welchen Messpunkt man in diese Funktionsgleichung einsetzt, ergeben sich geringe Abweichungen bei der Bestimmung von a.

z.B. für (15/66,8) erhält man a » -0,0111111

für (52,5/38,8) erhält man a » - 0,0110657

für (80/0) ergibt sich a » -0,0108281

Rundet man auf drei Dezimalstellen ergibt sich stets a » - 0,011. Also f(x) = -0,011x² + 69,3.

b) Die Messpunkte gibt man am besten über eine Matrix in das Computeralgebrasystem ein.

(In Derive über: Schreiben Matrix - wähle dann Zeilen 12 Spalten 2 und gib die entsprechenden Werte ein. Lass dann die Matrix zeichnen.) Plotte außerdem f.

Die Grafik zeigt nur sehr geringe Abweichungen. Der Parabelbogen wird sehr genau beschrieben.

c) Es ist lediglich eine Verschiebung um 80 Einheiten nach rechts auf der x-Achse durchzuführen. Also lautet die gesuchte Funktion g(x) = -0.011(x-80)² + 69,3. Ausmultipliziert erhält man g(x) = -0.011x² + 1,76x -1,1.