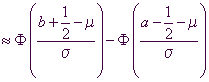< weiter>
<zurück>
<top>
Die Näherungsformel
von de Moivre - Laplace
Histogramme der
Binomialverteilung
< weiter>
<zurück>
<top>
Von dem französischen
Mathematiker de Moivre (1667-1754) stammt die Vermutung, dass man durch eine
"Standardisierung" alle Histogramme "unter einen Hut" bringen
kann:
|
1.
|
Man muss für alle Histogramme
die "Symmetrieachsen" zusammenlegen.
Dieses erreicht man durch Verschiebung
um 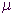 ( (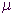 ist der Erwartungswert der Binomialverteilung) nach links.
ist der Erwartungswert der Binomialverteilung) nach links.
|
|
2.
|
Außerdem muss man unter
Beibehaltung des Flächeninhaltes
die Breite der Streifen geeignet verkleinern und die Höhe entsprechend
vergrößern.
Die flächeninvariante
Verformung der Histogramme wird erreicht, wenn man als Balkenbreite  und die Balkenhöhe
und die Balkenhöhe 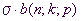 wählt.
( wählt.
( bezeichnet die Standardabweichung der Binomialverteilung
bezeichnet die Standardabweichung der Binomialverteilung 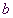 .) .)
|
< weiter>
<zurück>
<top>
"Standardisierte"
Histogramme und Gaußsche Dichtefunktion
< weiter>
<zurück>
<top>
Man erkennt, dass
bei passender Wahl der Parameter n und p die Mittelpunkte der oberen Begrenzungslinie
aller Rechtecke, also die Punkte 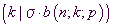 ,
ziemlich genau auf dem Graphen von
,
ziemlich genau auf dem Graphen von 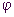 mit
mit
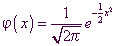 liegen.
liegen.
< weiter>
<zurück>
<top>
Lokale Näherungsformel
von Laplace:
Für 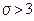 gilt:
gilt:
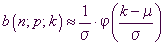 mit
mit 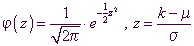 .
.
Die Funktion heißt 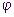 Gaußsche Dichtefunktion.
Gaußsche Dichtefunktion.
Anmerkung: Laplace (1749-1827) hat
im Jahre 1812 den schon von Moivre vermuteten Sachverhalt als erster streng
bewiesen. Der exakte Beweis hat "Hochschulniveau" und wird hier nicht
angegeben.
In den meisten Fällen benötig
man nicht die Wahrscheinlichkeit, dass ein bestimmtes Ereignis 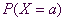 eintritt,
sondern die Wahrscheinlichkeit, dass das Ereignis in einem bestimmten Intervall
eintritt,
sondern die Wahrscheinlichkeit, dass das Ereignis in einem bestimmten Intervall
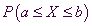 liegt.
liegt.
Die Wahrscheinlichkeit dafür
wird durch die Fläche der Säulen im Histogramm graphisch dargestellt.
Diese Fläche wird näherungsweise durch ein Integral bestimmt.
< weiter>
<zurück>
<top>
Gaußsche
Integralfunktion
Die durch 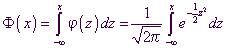 Funktion
Funktion
 heißt
Gaußsche Integralfunktion.
heißt
Gaußsche Integralfunktion.
Die Funktion 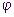 besitzt keine elementare Stammfunktion. Die Werte der Integralfunktion
besitzt keine elementare Stammfunktion. Die Werte der Integralfunktion  können
mithilfe eines CAS oder mithilfe von Tabellen bestimmt werden.
können
mithilfe eines CAS oder mithilfe von Tabellen bestimmt werden.
< weiter>
<zurück>
<top>
Globale Näherungsformel
von Laplace (Normalverteilung, Gaußsche Verteilung)
Für 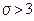 gilt:
gilt:
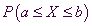
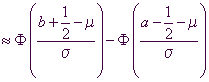
mit 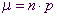 und
und 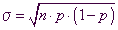 .
.
< weiter>
<zurück>
<top>
Beispiel:
Die Berechnungen zum Ausgangsbeispiel:
n = 244 ; p = 0,056 : 

Das Ergebnis entspricht ungefähr
den Berechnungen mithilfe der Binomialverteilung.
<
weiter> <zurück>
<top>
Vergleich
von Binomialverteilung und Normalverteilung
 Excel-Arbeitsblatt
zur Binomial- und Normalverteilung
Excel-Arbeitsblatt
zur Binomial- und Normalverteilung
<zurück>
<top>
![]() (
(![]() ist der Erwartungswert der Binomialverteilung) nach links.
ist der Erwartungswert der Binomialverteilung) nach links.![]() und die Balkenhöhe
und die Balkenhöhe ![]() wählt.
(
wählt.
(![]() bezeichnet die Standardabweichung der Binomialverteilung
bezeichnet die Standardabweichung der Binomialverteilung ![]() .)
.)