| Ergebnis | Wahrscheinlichkeit |
| Erfolg | |
| Misserfolg |
| Ergebnis | Wahrscheinlichkeit |
| EE | |
| EM | |
| ME | |
| MM |
| BERNOULLI-Versuche |
|
Arbeitsauftrag |
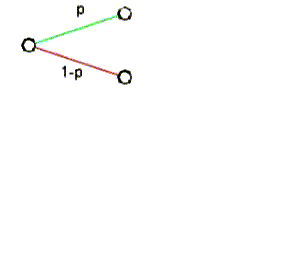
Darstellung und Analyse eines 1-stufigen bis 4-stufigen Bernoulli-Versuchs in einem Baumdiagramm
Das Baumdiagramm für den 2-stufigen Bernoulli-Versuch setzt sich aus zwei Baumdiagrammen 1-stufiger Bernoulli-Versuche und einer zusätzlichen Stufe zusammen.
| 1-stufig | 2-stufig | ||||||||||||||||
 |
|
||||||||||||||||
|
|
Zusammenfassung: Die Anzahl der Wege in einem Baumdiagramm von einem n-stufigen Bernoulli-Experiment, die zu k Erfolgen führen, wird hier mit bk(n,k) abgekürzt.
| Anzahl k der Erfolge | Zugehörige Ergebnisse | P(X=k) | ausführlich | |
|
0
|
M |
1
|
||
|
1
|
E |
1
|
2-stufig
| Anzahl k der Erfolge | Zugehörige Ergebnisse | P(X=k) | ausführlich | |
|
0
|
MM |
1
|
||
|
1
|
EM EM |
2
|
||
|
2
|
EE |
1
|
Darstellung eines 3-stufigen Bernoulli-Versuchs in einem Baumdiagramm. Das Baumdiagramm für den 3-stufigen Bernoulli-Versuch setzt sich aus zwei Baumdiagrammen 2-stufiger Bernoulli-Versuche und einer zusätzlichen Stufe zusammen.
| Baumdiagramm | Ergebnis | Wahrscheinlichkeit |
|
|
EEE |
|
|
EEM |
||
|
EME |
||
|
EMM |
||
|
MEE |
||
|
MEM |
||
|
MME |
||
| MMM |
| Anzahl k der Erfolge | Zugehörige Ergebnisse | P(X=k) |
|
1+0
|
EMM |
|
|
1+1
|
EEM EME |
|
|
1+2
|
EEE |
|
Tabelle zum unteren Teilbaum:
| Anzahl k der Erfolge | Zugehörige Ergebnisse | P(X=k) |
|
0+0
|
MMM |
|
|
0+1
|
MEM MME |
|
|
0+2
|
MEE |
|
Zusammenfassung der beiden Tabellen:
| Anzahl k der Erfolge | Zugehörige Ergebnisse | P(X=k) | ausführlich | |
|
0
|
MMM |
1
|
||
|
1
|
EMM MEM MME |
3
|
||
|
2
|
EEM EME MEE |
3
|
||
|
3
|
EEE |
1
|
Darstellung eines 4-stufigen Bernoulli-Versuchs in einem Baumdiagramm.
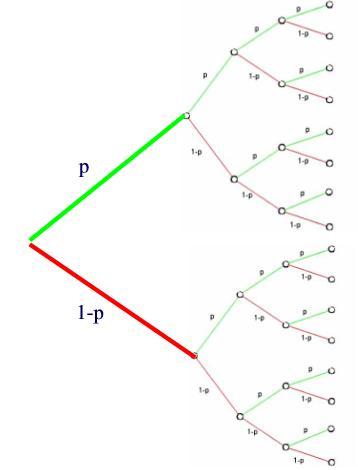 |
Das Baumdiagramm für den 4-stufigen Bernoulli-Versuch setzt sich aus zwei Baumdiagrammen 3-stufiger Bernoulli-Versuche und einer zusätzlichen Stufe zusammen. Das Baumdiagramm aus dem 3-stufigen Versuch ist hier zweimal in das neue Bild kopiert worden. |
| Anzahl k der Erfolge | Zugehörige Ergebnisse | P(X=k) |
|
1+0
|
EMMM |
|
|
1+1
|
EEMM EMEM EMME |
|
|
1+2
|
EEEM EEME EMEE |
|
|
1+3
|
EEEE |
|
Tabelle zum unteren Teilbaum:
| Anzahl k der Erfolge | Zugehörige Ergebnisse | P(X=k) |
|
0+0
|
MMMM |
|
|
0+1
|
MEMM MMEM MMME |
|
|
0+2
|
MEEM MEME MMEE |
|
|
0+3
|
MEEE |
|
Zusammenfassung der beiden Tabellen:
| Anzahl k der Erfolge | Zugehörige Ergebnisse | P(X=k) | ausführlich | |
|
0
|
MMMM |
1
|
||
|
1
|
MEMM MMEM MMME EMMM |
4
|
||
|
2
|
MEEM MEME MMEE EEMM EMEM EMME |
6
|
||
|
3
|
MEEE EEEM EEME EMEE |
4
|
||
|
4
|
EEEE |
1
|
|
vorhergehende Stufe (n-1)
|
Anzahl der Pfade mit (k-1) Erfolgen
|
+
|
Anzahl der Pfade mit k Erfolgen
|
|
neue Stufe n
|
|
Mißerfolg |
|
|
Anzahl der Pfade mit k Erfolgen
|
bk(n,k) = bk(n-1,k) + bk(n-1,k-1) ; bk(n,0) = 1; bk(n,n) = 1
Alle Zufallsversuche mit k Erfolgen in den vorhergehenden Stufen und einem Mißerfolg in der neuen Stufe und alle Zufallsversuche mit (k-1) Erfolgen in den vorhergehenden Stufen und einem Erfolg in der neuen Stufe führen zu insgesamt k Erfolgen in allen Stufen zusammen.
Man berechnet also die Wahrscheinlichkeit, dass bei einem n-stufigen Bernoulli-Experiment k-mal ein Erfolg eintritt, durch folgende Formel:
![]()
Der Faktor bk(n,k) heißt Binomialkoeffizient.
Berechnungsmöglichkeiten von bk(n,k):
| Taschenrechner | |
 |
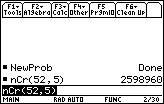 nCr(52,5) nCr(52,5) |
 |
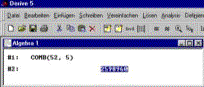 COMB(52,5)
COMB(52,5) |
|
|
=KOMBINATIONEN(52;5) |