Teilaufgabe 3:
|
In diesem Falle liegen die Punkte P1(-6/18) und P3(18/-6)
weder auf der Geraden  noch
auf der Geraden 
|
|
|
Die Fixpunktgerade hat die Gleichung: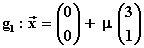 
die Fixgerade die Gleichung: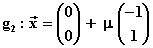 
|
|
|
| Wie man leicht sieht, streben die Punktfolgen P1,
P1', P1'', P1''' ...... und P3, P3', P3'', P3''',..... gegen den
Punkt Q(9/3) |
|
Drücken wir die Ortsvektoren zu den Punkten P1 und P3 als
läßt Linearkombination der Eigenvektoren aus, so ergibt
sich:
|
 =  |
 = 
|
|
Wenden wir auf beide Vektoren die Abbildungsmatrix
A an, so ergibt sich:
|
|
|
|
|
|
Der Anteil des Ortsvektors in Richtung des Eigenvektors  bleibt
unverändert, die Komponente des Ortsvektors in Richtung 
wird um den Faktor 0,8 verkürzt. |
| Da dies bei jeder weiteren Abbildung durch die Matrix A in gleicher
Weise geschieht, bleibt letztlich der Anteil in Richtung konstant,
der in Richtung konvergiert
gegen den Ursprung (siehe Teilaufgabe 2) |
| Insgesamt konvergieren also beide Punktfolgen
gegen den Punkt Q(9/3). |
|
