Für die Fixgerade, bzw. ergibt
sich bei der Iteration das folgende Bild:
Man erkennt leicht, das z.B. die Bildpunkte ( P', P''. P''',.....)
des Punktes P(-12/12) mit jeder weiteren Abbildung natürlich
auf der Geraden liegen,
aber sich dem Ursprung nähern. Dabei wird mit jeder weiteren
Abbildung die Länge des Vektors um
den Faktor (
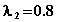Eigenwert) verkürzt.
Die Punktfolge P, P',P'',P''.....
konvergiert also gegen den Ursprung
Die Punktfolge Q, Q', Q'', Q''',..... konvergiert ebenfalls
gegen den Ursprung
Mathematische Betrachtungen:
Ein Punkt gehört zur Geraden, wenn die Spitze seines Ortsvektors
auf
der Geraden liegt. Für jeden Wert von ergibt
sich ein anderer Punkt P; d.h. für jeden festen Wert
von
ergibt sich ein fester Ortsvektor. Auf Vektoren können wir
aber die Matrix anwenden.
Wenden wir also die Matrix A auf die Gleichung: der
Fixgeraden an, ergibt sich
für jeden Ortsvektor: :
Ergebnis: Für alle Punkte die auf
der Fixgeraden liegen gilt: Ihre
Ortsvektoren werden durch die Abbildungsmatrix A um den Faktor
0,8 verkürzt, ihre Richtung und Orientierung bleibt unverändert
, bzw. 
ergibt
sich bei der Iteration das folgende Bild:
liegen,
aber sich dem Ursprung nähern. Dabei wird mit jeder weiteren
Abbildung die Länge des Vektors 
um
den Faktor 
(
Eigenwert) verkürzt.
ergibt
sich ein anderer Punkt P; d.h. für jeden festen Wert
von 
