Aufgabe I:

In einem kleinen Land gibt es ca. 1 000 000 Erwerbstätige, die vom Finanzamt jährlich einer der drei Einkommensgruppen (niedrig, mittel, hoch ) zugeordnet werden. Der Stichtag für die Einordnung ist der 1.Januar eines jeden Jahres.

Es hat sich im Laufe der Jahre gezeigt, dass es zwischen diesen Gruppen Verschiebungen gibt.

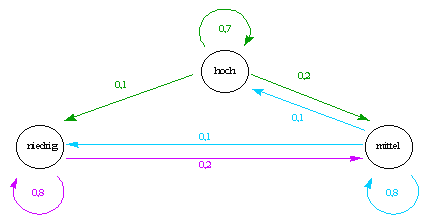
Die Pfeile im Diagramm geben für jede Einkommensgruppe an, welche Anteile dieser Gruppe von einem Jahr zum nächsten die Gruppe wechseln bzw. in der Gruppe bleiben.

Auftrag:

1. Bestimme die Übergangsmatrix.
2. Berechne die Anzahl der Erwerbstätigen, die sich am nächsten Stichtag in diesen Gruppen befinden.
3. Bestimme die Stärken der Gruppen für weitere 2 Jahre.
4. Stelle die Übergänge in den Einkommensgruppen für den Zeitraum von zwei Jahren in einem Baumdiagramm dar und berechne daraus die Übergangsmatrix für diesen Zeitraum.
5. Berechne die Übergangsmatrix A² und vergleiche mit dem Ergebnis aus (4).
6. Bestimme die Matrizen A³ und A⁴.
7. Falls Du ein CAS zu Verfügung hast, bestimme A¹⁰, A¹⁵ und A²⁰. Was fällt Dir auf?
8. Bestimme den "stabilen Vektor" durch das Lösen eines geeigneten Gleichungssystems.
9. Bestimme dann die Grenzmatrix.

Erweiterung

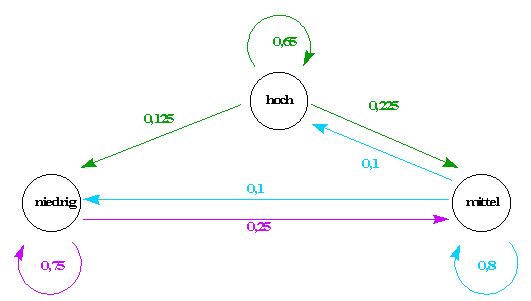
Durch neue Programme von Politik und Wirtschaft wird versucht, das Einkommen breiter Schichten der Bevölkerung zu verbessern. Man erhofft sich, dass sich die Übergänge wie folgt verändern:

Auftrag:

1. Untersuche, welche Auswirkungen diese Veränderungen auf den stabilen Vektor haben und vergleiche die Ergebnisse mit denen der Ausgangsverteilung
2. Versuche selbst durch Wahl geeigneter Übergänge die Situation positv zu beeinflussen.

   (Die Arbeit mit einem CAS ist unbedingt zu empfehlen!)

ergebnisse