a) Die Übergangsmatrix ist eine stochastische Matrix, d.h. die Summe der Komponenten jeder Spalte ist 1. Die Matrixelemente ergeben sich direkt aus den Prozentzahlen der Aufgabenstellung.
Für die Besucherverteilungen ergeben sich
nach einer Stunde   = , nach zwei Stunden = , und nach drei Stunden = .

b) Der Ansatz führt auf ein lineares Gleichungssystem mit den beiden Koordinaten des Vektors als Unbekannte. Die Lösung lautet x =1,5 y.
Mit der zusätzlichen Bedingung x + y = 1200 erhält man den Fixvektor bzw. die Fixverteilung .

*c) Induktionsverankerung mit n = 0 oder n = 1:
n = 0 entspricht der Anfangsverteilung
n = 1 stimmt mit dem Ergebnis aus a) überein

Induktionsschritt von n auf n+1:
zu zeigen ist: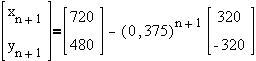
Umformen der linken Seite der Behauptung ergibt unter Ausnutzung der Fixverteilung aus b):
.
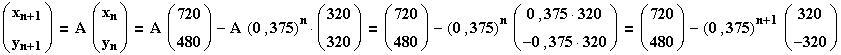Der letzte Term entspricht der rechten Seite der Behauptung.

d) Die Grenzverteilung erhält man mithilfe der Gesetzmäßigkeit aus c) wie folgt:.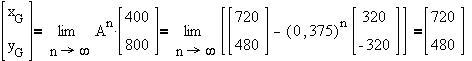
Die Grenzverteilung ist mit der Fixverteilung identisch.
Da es bei dieser Verteilung um Menschen geht, sollte sinnvollerweise auf ganze Zahlen gerundet werden.
Probieren liefert, dass die Grenzverteilung theoretisch nach 7 Stunden erreicht wird, was einer Uhrzeit von 21:00 Uhr entspricht.

e) Der Ansatz führt auf das lineare Gleichungssystem

I     ( 0,75 - )x + 0,375y = 0
II    0,25x + (06,25 - )y = 0

Da sowohl x als auch y von 0 verschieden sein müssen, führt die Lösung des Gleichungssystems auf:

Diese quadratische Gleichung liefert die beiden Eigenwerte 1 und 0,375.

f) Die Anfangsverteilung kann man mithilfe der inversen Matrix von A bestimmen. A ist invertierbar, da die Spaltenvektoren dieser quadratischen Matrix linear unabhängig sind, wie man sofort sieht. Dies kann man natürlich auch an den Zeilen überprüfen.
Die inverse Matrix lautet .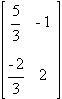
Zweimaliges Anwenden auf die gegebene Verteilung nach zwei Stunden liefert die gesuchte Anfangsverteilung. Zu Beginn des Schulfestes fanden sich also 360 Besucher in der Aula und 720 Besucher im Freien.