| Station 3 | Lösungen: Mehrstufige Produktionsprozesse |
a) Der Rohstoffbedarf für das Bauteil B2 wird wie folgt berechnet:
| Rohstoff R1: | |
| Rohstoff R2: | |
| Rohstoff R3: | |
| Rohstoff R4: |
b) Die Tabelle ergibt sich durch Multiplikation von zwei Matrizen. Dabei
sei A die Matrix, die den Rohstoffbedarf für die einzelnen Teile
angibt. B sei die Matrix, die zeigt, wie viele der Teile für die
einzelnen Baugruppen benötigt werden. Es gilt dann:
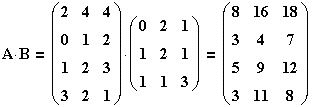
In der 1. Spalte finden Sie den jeweiligen Rohstoffbedarf für das Bauteil B1, entsprechend finden Sie in Spalte 2 den Rohstoffbedarf für Teil B2 (siehe Rechnung bei a) ).
c) Um den Rohstoffbedarf für die beiden Endprodukte zu berechnen, wird die Ergebnismatrix aus b) mit der Matrix C, die die benötigten Bauteile für die Endprodukte P1 und P2 angibt, multipliziert.

In der ersten Spalte finden Sie die benötigten Rohstoffmengen für das Endprodukt P1 in der zweiten Spalte finden Sie die Rohstoffmengen für das zweite Endprodukt.
d) Für die
Berechnung des Rohstoffbedarfs für die beiden Endprodukte hat man
zwei Möglichkeiten:
Man multipliziert zunächst die Matrizen A und B und dieses Produkt
dann mit der Matrix C (siehe Aufgabe c) oder man multipliziert zunächst
die Matrizen B und C und dieses Produkt dann von links mit der Matrix
A. Für die Matrizenmultiplikation gilt nämlich das Asssoziativgesetz:
![]()
e) Wenn man berechnen will, wie viele Endprodukte mit den gegebenen Rohstoffmengen hergestellt werden können, muss man das folgende lineare Gleichungssystem (hier in Matrix-Vektor-Schreibnweise dargestellt) lösen.
Hinweis: Dieses Gleichungssystem besteht aus 4 Gleichungen mit 2 Variablen. Falls Sie bisher solche Gleichungssysteme noch nicht behandelt haben, lösen Sie zunächst ein Gleichungssystem mit 2 Gleichungen und 2 Variablen und überprüfen Sie, ob die gefundenen Lösungen auch die anderen beiden Gleichungen erfüllen.
 |
|
| Als Lösungsvektor ergibt sich: |  |
Es können
also 15 mal das Produkt P1 und 25 mal das Produkt P2
hergestellt werden.
| zurück |
