Zur MathePrisma-Startseite
Zur Modul-Startseite  


Kombinatorik (Einleitung 2 )
 

  
 
  
Lösung:
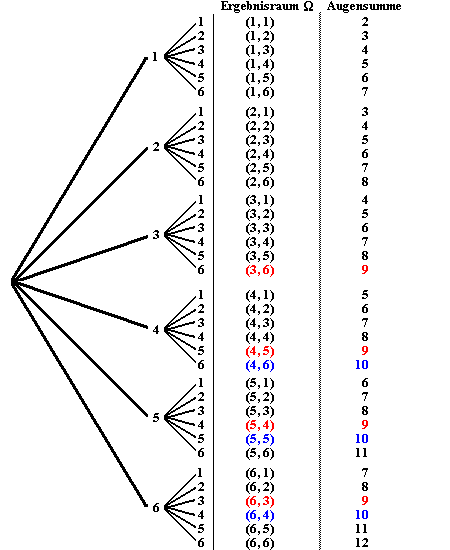
 Tatsächlich gibt es folgende Möglichkeiten für die Augensumme neun:

(3,6) (6,3) (4,5) (5,4)

und für die Augensumme zehn:

(4,6) (6,4) (5,5)

9 und 10 lassen sich zwar beide nur auf zwei Arten als Summe von Würfelzahlen schreiben, wenn man nicht auf die Reihenfolge der Summanden achtet. Achtet man aber auf diese, dann gibt es vier bzw. drei Arten.
Man muss daher also die geordneten Paare an Würfelzahlen zählen, welche 9 bzw. 10 ergeben.

 
  
 
 Sie können sich diesen Sachverhalt auch mit einem Baumdiagramm veranschaulichen.
 
  
Alternativ : ein Baumdiagramm
 
  
 
 Im Eingangsbeispiel ging es darum, Anzahlen von Möglichkeiten richtig zu bestimmen. Dabei kommt man mit einem einfachen Baumdiagramm aus. Will man aber beispielsweise die Anzahl aller möglichen Ziehungen beim Samstagslotto bestimmen, so könnte das entsprechende Baumdiagramm doch recht umfangreich werden …

Kombinatorik
 Hilfreich für die richtige Berechnung der Anzahl von Möglichkeiten ist das mathematische Gebiet der Kombinatorik.
In der Kombinatorik werden verschiedene Abzählvorgänge systematisiert und in "Formeln" gefasst.
Bei sachgemäßer (!) Anwendung der Kombinatorik wird es nicht mehr geschehen, dass ein Element vergessen (wie in unserem Einstiegsbeispiel) oder mehrfach gezählt wird.
 
  
Seite 2/8