Koordinatengeometrie - Lineare Funktionen und ihre Graphen |
Lösung |
Abstand eines Punktes zu einer Geraden: Lösung zu Aufgabe 10.4
Der kürzeste Abstand d des Punktes P(5 | 11) von der Geraden g (aus 10.1) lässt sich folgendermaßen berechnen:
Man berechnet :
Eine Lösung mit DERIVE finden Sie unter Aufgabe10-4.mth.
(Die Gerade g hat die Steigung m1 = 0,5.)
m1 · m2 = -1
Û 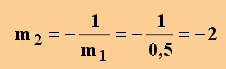
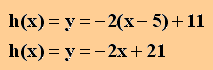
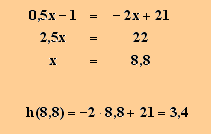
Also S(8,8 | 3,4).
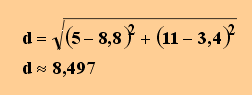
|
|
|