Koordinatengeometrie - Lineare Funktionen und ihre Graphen

Hilfe

Abstand eines Punktes zu einer Geraden: Hilfe 3 zu Aufgabe 10.4

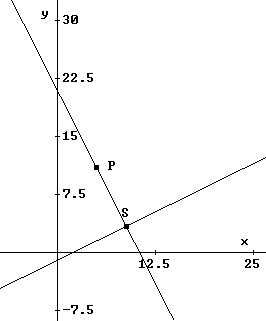
Um den gesuchten Abstand des Punktes P zur Geraden g zu bestimmen, müssen Sie folgende Teillösungen berechnen.

• die Gleichung h(x) der zu g orthogonalen Geraden durch den Punkt P(5/11),
  
  
• den Schnittpunkt S der Graphen (Geraden) zu  g und h (mit DERIVE berechnen!);
   
  
• den Abstand d von S zum Punkt P mit der Abstandsformel (mit DERIVE berechnen!).