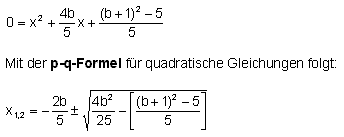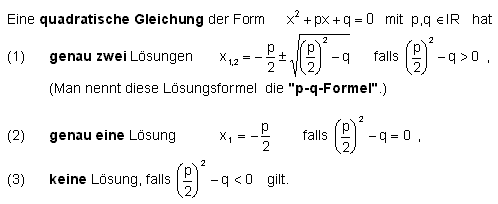Koordinatengeometrie - Lineare Funktionen und ihre Graphen

Hilfe

Tangente am Kreis: Hilfe 3 zu Aufgabe 14.3

Durch Einsetzen des Geradenterms in die Kreisgleichung entsteht nun eine quadratische Gleichung:

Zur Erinnerung:

Damit der Kreis mit der Tangente genau einen Schnittpunkt hat, muss der Term unter der Wurzel gleich Null sein.

Setzen Sie den Term unter der Wurzel (sogenannte "Diskriminante") gleich Null und lösen Sie die neue entstehende quadratische Gleichung (mit Variable b) mit p-q-Formel.

ANMERKUNG:

Man kann auch die quadratische Gleichung

durch DERIVE nach x auflösen lassen. DERIVE gibt dann die beiden Lösungen, die man auch mit der p-q-Formel erhält, getrennt an. Dann muss man erkennen, dass sich die Lösungen für x nur im Vorzeichen vor der Wurzel unterscheiden. D.h. die beiden Lösungen sind identisch, wenn der Term unter der Wurzel Null ist, und es gibt keine Lösung, wenn der Term unter der Wurzel kleiner Null ist. Sonst gibt es zwei Lösungen. Ab jetzt geht man so vor wie oben, indem man den Term unter der Wurzel gleich Null setzt.