Koordinatengeometrie - Lineare Funktionen und ihre Graphen |
Baustein 1 - 5(10) |
Das Zeichnen von Geradenstücken mit DERIVE: Die Chi-FunktionUm nicht die gesamte Gerade sondern nur ein Teilstück anzuzeigen, bedienen wir uns eines "Kunstgriffs". Die Mathematik liefert uns die sogenannte Chi-Funktion. Diese
setzt außerhalb eines vorgegebenen Intervalls alle Werte auf
Null. Innerhalb des Intervalls setzt sie die Werte auf Eins. Multipliziert
man nun eine Funktion f mit der Chi-Funktion, so sind alle Werte
außerhalb des Intervalls Null und alle Werte innerhalb des
Intervalls entsprechen den Funktionswerten der Funktion f. |
||
|
Die Geraden, die Sie in Teilaufgabe 2.1 bestimmt haben, sind nur für bestimmte Abschnitte zugelassen, z. B. die Gerade zu F1(x) im Bereich 0 £ x £ 300. Da Sie die Geraden später abschnittsweise ("piecewise") mit dem Programm DERIVE zeichnen sollen, üben Sie hier schon einmal den Umgang mit der sogenannten CHI-Funktion [CHI(a,x,b)*F(x)] : Beispiel: F(x): = 0.5x - 2 soll im Bereich von x = 2 bis x = 10 gezeichnet werden. Dann ist im Programm DERIVE einzugeben: CHI(2,x,10)*F(x)
|
||
|
Aufgabe 2 (Fortsetzung) |
||
|
2.2 |
Formulieren Sie die entsprechenden CHI-Funktionen für die Geraden aus Aufgabe 2.1 ! | |
|
Die folgenden Aufgaben sollen mit dem Computer-Algebra-System DERIVE bearbeitet werden! Bevor Sie das Programm DERIVE starten, hier Ihre Aufgabe:
|
||
|
2.3 |
Geben Sie zunächst die Funktionen F1,
... , F5, G1, ... . G4 aus Aufgabe 2.1 mittels des DERIVE -Befehls
"Author" bzw. "Author Expression" im
Algebra-Fenster ein. Wenden Sie dann für jedes einzelne Geradenstück die Chi-Funktion an und addieren Sie die einzelnen Produkte: CHI(...)*F1(x)+...+CHI(...)*F5(x) bzw. CHI(...)*G1(x)+...+CHI(...)*G5(x) (Die Addition ist ein weiterer "Kunstgriff" und lässt sich bei stückweise linearen Funktionen, also bei aus Geradenstücken zusammengesetzten Funktionsgraphen, immer anwenden. Bei anderen stückweise definierten Funktionen versagt dieser "Kunstgriff" und die Funktionsstücke müssen in DERIVE einzeln nacheinander gezeichnet werden.) |
|
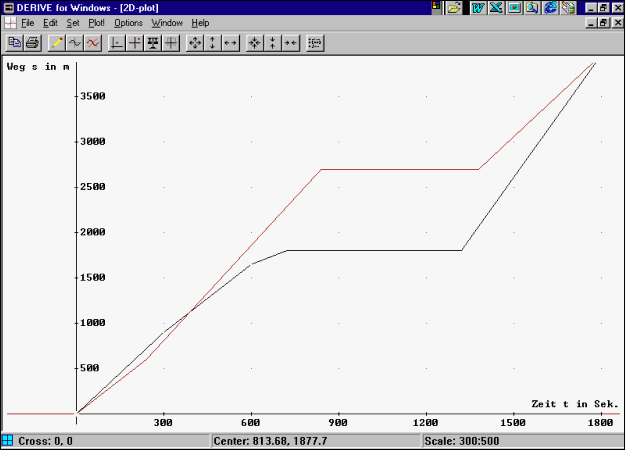
| Wechseln Sie dann ins Graphikfenster
von DERIVE und plotten (zeichnen) Sie die beiden obigen Funktionen.
Auf Ihrem Bildschirm müssten Sie dann folgendes sehen können (eventuell
müssen Sie noch die Einstellungen mit dem Befehl "Set"
ändern, die Sie am unteren Bildrand ablesen können): Set>Center: Horizontal: 813.68 Vertical: 1877.7 Set>Cross: Horizontal: 0 Vertical: 0 Set>Range: Top: 4000 Left: - 175 Right: 1800 Bottom: - 250 Set Scale: Horizontal: 300 Vertical: 500 |
||
|
Minimieren Sie nun den Internet Browser (oben rechts, linker Button) und rufen Sie das Programm DERIVE auf ! Kehren Sie danach wieder in den Lehrgang zurück!
|
||