Übungsaufgaben: Lösung zu Aufgabe
9
Da es sich um eine ganzrationale Funktion
4. Grades handelt, deren Graph symmetrisch zur y-Achse verläuft,
macht man für die Funktionsgleichung den Ansatz: f(x)
= a·x4 + b·x2 +
c mit a, b,
c ÎIR.
Die erste Ableitung der Funktion f zu f(x)
= a·x4 + b·x2 +
c lautet
dann: f '(x) =
4·a·x3
+ 2·b·x
Damit ergibt sich:
(1) f(0) = 0 Û
a·04
+ b·02 + c = 0 Û
c = 0
(2) f(3) = 0 Û a·34
+ b·32 + c = 0 Û
81a + 9b = 0
(3) f '(3) = - 48 Û 4·a·33
+ 2·b·3
= - 48 Û 108a
+ 6b = - 48
DERIVE liefert als Lösung dieses Gleichungssystems:
(Dazu verwendet man den Befehl SOLVE([F(0)=0,F(3)=0,...],[a,b,c])
oder man löst das obige Gleichungssystem mit dem Befehl Solve > System.)
Die Berechnungen hierzu finden Sie im DERIVE-File
Übungsaufgabe
9.mth
im Anhang!
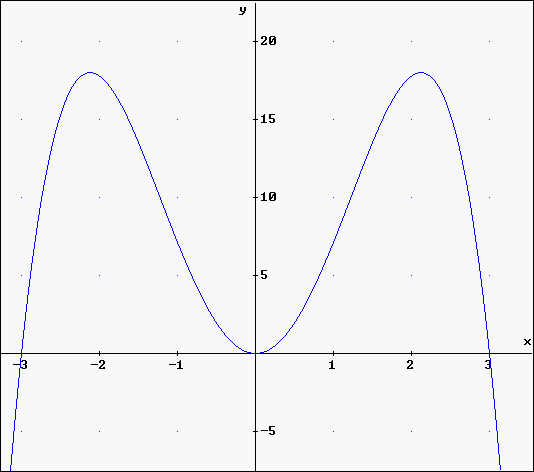
Ausdruck des Graphen zu f:
|
