Differentialrechnung - Bestimmung von Funktionsgleichungen |
Lösung |
Übungsaufgaben: Lösung zu Aufgabe 16b
Die Funktionsgleichung aus Aufgabenteil a lautet:
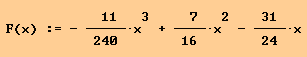
Gesucht ist der Zeitpunkt, zu dem das Fieber am niedrigsten ist,
d.h. eine Tiefstelle der Funktion.
Man macht daher den Ansatz
f '(x)= 0
und löst die Gleichung
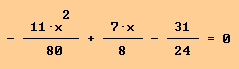
Lösungen sind zunächst
x1 » 2,327 und x2 » 4,036
Der Wert x2 liegt außerhalb des zu untersuchenden Bereichs.
Der Wert x1 muss noch in die zweite Ableitung eingesetzt werden, um zu überprüfen, ob tatsächlich eine Tiefstelle vorliegt.
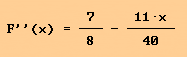
liefert f ''(2,327) » 0,235.
An der Stelle x1 liegt demnach ein Tiefpunkt vor.
Die dort erreichte maximale Fiebersenkung errechnet man nun durch Einsetzen in f(x).
f(2,327) » -1,214.
Die Maximale Fiebersenkung erreicht man nach etwa 2 Stunden und 20 Minuten und das Fieber kann um 1,214oC gesenkt werden.
(0,327 Stunden * 60 Minuten/Stunde =19,6 Minuten » 20 Minuten)
Die Berechnungen hierzu finden Sie im DERIVE-File Übungsaufgabe 16.mth im Anhang!
|
|
|