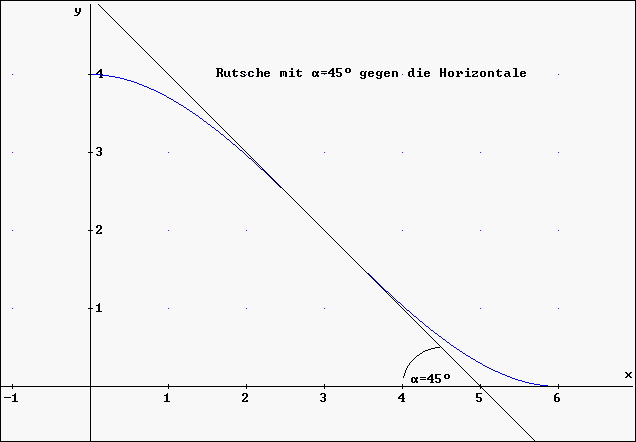
Rutsche: Lösung zu Aufgabe 2.4

Die 6 Bedingungen, die auf Gleichungen führen, sind:
(1) f(0) = 4
(2) f '(0) = 0
(3) f(e) = 0
(4) f ' (e) = 0
(5) f ''(e/2) = 0 (die steilste Stelle ist aus Symmetriegründen bei der Wendestelle x_w = e/2 )
(6) f '(e/2) = - 1 (denn die Steigung der Tangente muss tan(45^o)= - 1 sein, da der Winkel 45^o ist )

Der Ansatz für eine ganzrationale Funktion f   3. Grades lautet:
f(x)=a·x³ + b·x² + c·x + d    mit a, b, c, d ÎIR.
Þ f '(x) = 3ax² + 2bx + c    
Þ f ''(x) = 6ax + 2b   

Umformung der Gleichungen unter Anwendung von f(x), f '(x) und f ''(x) ergibt:

(1) f(0) = 4 Û a·0³ + b·0² + c·0 + d = 4 Û d= 4
(2) f '(0) = 0 Û 3·a·0² + 2·b·0 + c = 0 Û c = 0
(3) f(e) = 0 Û a·e³ + b·e² + c·e + d = 0 Û a·e³ + b·e² + 4 = 0
(4) f '(e) = 0 Û 3·a·e² + 2·b·e + c = 0 Û 3·a·e² + 2·b·e = 0
(5) f ''(e/2) = 0 Û 6·a·(e/2) + 2·b = 0 Û 3·a·(e/2) + 2·b = 0 Û 3·a·e² + 2·b·e = 0 (vgl. (4) ! )
(6) f '(e/2) = - 1 Û 3·a·(e/2)² + 2·b·(e/2) + c = - 1 Û 0.75·a·e² + b·e = - 1

Die Gleichungen führen nun auf ein nicht-lineares Gleichungssystem mit 3 Gleichungen und den 3 Unbekannten a, b und e (wobei c = 0 und d = 4 sofort benutzt wird) und sich nicht mit DERIVE lösen lässt:

(1) a·e³ + b·e² + 4 = 0
(2) 3·a·e² + 2·b·e = 0
(3) 0,75·a·e² + b·e = - 1

Formt man nun (2) um, so ergibt sich: (4) a·e³ = - (2/3)·b·e²

Setzt man nun (4) in (1) ein, so folgt: (5) b·e² = - 12

(5) in (4) eingesetzt ergibt dann: (6) a·e³ = 8

Formt man nun (3) um, so ergibt sich: (7) 0,75·a·e³ + b·e² = - e

Setzt man nun (6) und (5) in (7) ein, so erhält man als erste Lösungsvariable: e = 6

Also muss setzt die Rutsche e = 6m vom Leitergerüst am Boden auf.
Zur Bestimmung der Funktionsgleichung:

e=6 einsetzen in (5) bzw. (6) ergibt dann: b = -1/3 und a = 1/27 .

Daher ist die gesuchte Funktionsgleichung für eine TÜV-gerechte Rutschbahn mit einem Winkel von  45^o gegen die Horizontale:

Ausdruck im Graphik-Fenster von DERIVE :