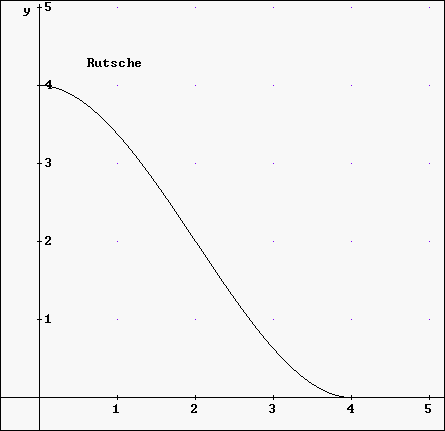
Rutsche: Lösung zu Aufgabe 2.2

Aus den vier Bedingungen ergibt sich folgendes lineare Gleichungssystem mit 4 Gleichungen und 4 Unbekannten:

(1) f(0) = 4 Û a·0³ + b·0² + c·0 + d = 4 Û d= 4
(2) f(4) = 0 Û a·4³ + b·4² + c·4 + 4 = 0 Û 64a + 16b + 4c + 4 = 0
(3) f '(0) = 0 Û 3a0² + 2b·0 + c = 0 Û  c = 0  
(4) f '(4) = 0 Û 3a4² + 2b·4 + c = 0 Û 48a + 8b + c = 0

Vereinfacht man das Gleichungssystem weiter, so ergibt sich (nach Vertauschung der Reihenfolge):

(1) d = 4
(2) c = 0
(3) 64a + 16b = - 4
(4) 48a + 8b = 0

DERIVE liefert als Lösung dieses Gleichungssystems ( Gleichungen (3) und (4) betrachten! ):

Daher ergibt sich als gesuchte Funktionsgleichung für f:

Um nun den Graphen zu f im Bereich 0 £ t £ 4 zu zeichnen, verwendet man die CHI-Funktion .
Die Berechnungen hierzu finden Sie im DERIVE-File "Rutsche.mth" im Anhang!