Differentialrechnung - Bestimmung von Funktionsgleichungen |
Grundlagen |
"Die Gerade g mit g(x) = mx + b berührt den Graphen zu f an der Stelle x0 " bedeutet:
Die Gerade g
ist eine Tangente an den Graphen zu f an der Stelle x0.
Damit hat f an der Stelle x0 die Tangentensteigung m.
d. h.
f '(x0) = m .
Außerdem haben die Graphen von g und f an der Stelle
x0 einen Punkt gemeinsam.
d.h.
f(x0)=g(x0),
also
f(x0)=m · x0 +b
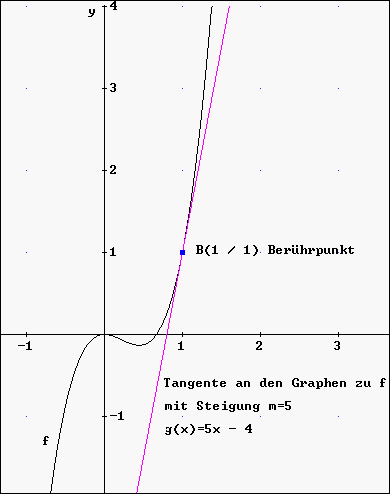
Beispiel: Der Funktionsgraph f zu f(x) = 3x3 - 2x2 hat an der Stelle x0 = 1 die Tangente g mit der Gleichung g(x) = 5x - 4 , denn es gilt: f '(1) = 5 = m . Des Weiteren haben die beiden Graphen an der Stelle x0 = 1 einen gemeinsamen Punkt, nämlich den Punkt B(1/1) (vgl. mit untenstehendem Graph):
|
|
|