Differentialrechnung - Bestimmung von Funktionsgleichungen |
Grundlagen |
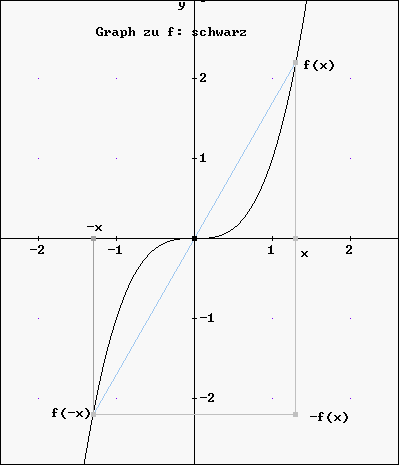
"Der Graph zu f ist punktsymmetrisch zum Ursprung" bedeutet:
- f(x) = f(-x) für alle x Î ID(f).
Anschaulich: Der Ursprung ist (Punkt-)Spiegelzentrum.
Beispiel: Der Graph zur Funktion
f mit der Gleichung f(x) = x3 ist symmetrisch (spiegelbildlich)
zum Ursprung:
Für jede (beliebige) Zahl x aus der Definitionsmenge ID(f)
gilt nämlich:
- f(x) = - x3 = (-x)3 = f(-x)
Vergleichen Sie auch mit untenstehendem Graph:
Da hier die Funktion f
eine ganzrationale Funktion sein soll, folgt:
Die Funktionsgleichung
von f enthält nur Potenzen mit ungeraden
Exponenten.
Daher lässt
sich ein vereinfachter Ansatz für
die gesuchte Funktion machen:
z. B. für eine ganzrationale Funktion 5. Grades:
f(x)=a·x5 +b·x3+ c·x mit
a, b, c Î IR
.
![]()
|
|
|