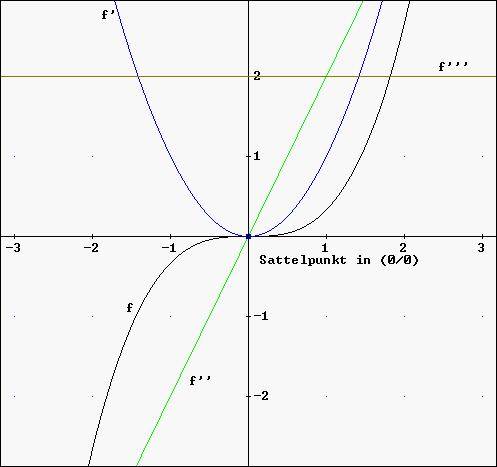Differentialrechnung - Kriterien der Kurvendiskussion - Sattelpunkt |
Grundlagen |
Ein Sattelpunkt ist notwendig
ein Wendepunkt mit einer waagerechten
Tangente.
Daher müssen beim Sattelpunkt S(x0
/ y0) die erste und die zweite
Ableitung
an der Stelle x0 Null sein.
Eine hinreichende Bedingung lautet: f '(x0) = 0 Ù f ''(x0) = 0 Ù f '''(x0) ¹ 0 .
Beispiel einer Funktion f mit zwei Sattelpunkten:
![]()
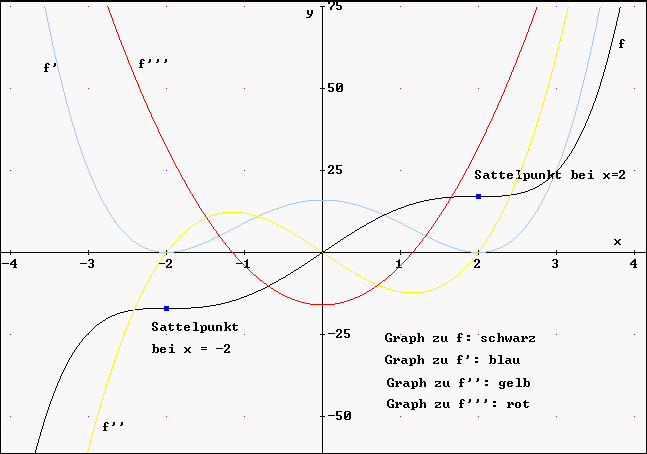
Ein weiteres Beispiel
zeigt ebenso den Zusammenhang zwischen dem Graphen
zu f und den Graphen der Ableitungsfunktionen:
|
|
|