Differentialrechnung - Bestimmung von Funktionsgleichungen |
Grundlagen |
"Der Graph zu f hat die Wendetangente g mit g(x) = mx + b an der Stelle x0 " bedeutet:
Der Graph zu f hat eine Wendestelle
an der Stelle x0 und gleichzeitig
dort eine Tangente
mit der Steigung m, d. h.
f '(x0) = m Ù f ''(x0) = 0 .
Außerdem haben die Graphen
von Funktion und Wendetangente an der Stelle x0 einen
gemeinsamen Punkt, d.h. f(x0)=g(x0).
Also
f (x0) = m · x0 + b.
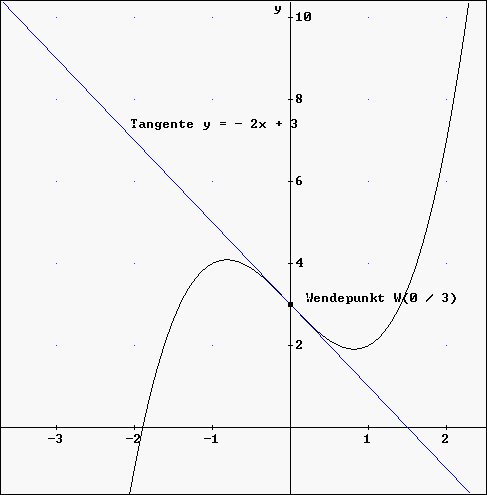
Beispiel:
Der Funktionsgraph f zu f(x) = x3 - 2x + 3 hat an der Stelle x0
= 0 die Wendetangente
mit
der Gleichung g(x) = y = -
2x + 3. Es gilt daher:
f '(0) = -2 und f
''(0) = 0 und f(0) = [-2 · 0 + 3 =] 3.
|
|
|