Differentialrechnung - Bestimmung von Funktionsgleichungen |
Baustein 4 (1-20) |
Alle Übungsaufgaben auf einen Blick (für Ausdruck auf Papier):
Innermathematische Steckbriefaufgaben:
1.)
Der Graph einer ganzrationalen Funktion f 3. Grades hat in P(1 / 4) eine
Tangente parallel zur x-Achse und in Q(0 / 2) einen Wendepunkt.
2.) Der Graph einer ganzrationalen
Funktion f 3. Grades verläuft durch P(0 / -5) und Q( 1 / 0)
und er berührt die x-Achse im Punkt R(5 / 0).
3.) Der Graph einer ganzrationalen
Funktion f 5. Grades ist symmetrisch zum Ursprung und besitzt in
P(-1/ 1) einen Wendepunkt mit der Steigung 3.
4.) Der
Graph einer ganzrationalen Funktion f 4. Grades ist symmetrisch
zur y-Achse. Im Punkt P(2 / 0) hat der Graph zu f die Steigung 2 und im
Punkt W(-1 / yw) einen Wendepunkt.
5.) Der
Graph einer ganzrationalen Funktion f 3. Grades verläuft durch
den Ursprung des Koordinatensystems. Im Punkt P(1 / 1) hat die Funktion
ein Extremum und im Punkt W(3 / yw) einen Wendepunkt.
6.) Der
Graph einer ganzrationalen Funktion f 4. Grades hat im Ursprung
des Koordinatensystems die Wendetangente mit der Gleichung y=x und im
Punkt P(2 / 4) die Steigung Null.
7.) Der Graph einer ganzrationalen
Funktion f 3. Grades ist symmetrisch zum Ursprung des Koordinatensystems
und verläuft durch den Punkt P(1 / -1). An der Stelle x=2 liegt ein
Extremwert vor.
8.) Eine ganzrationale Funktion f 3.
Grades hat an der Stelle x = - 1 eine Nullstelle. Der Graph zu f schneidet
die y-Achse bei 2 und berührt die x-Achse an der Stelle x=2.
9.) Der Graph einer ganzrationalen Funktion f 4. Grades ist symmetrisch
zur y-Achse. Er verläuft ferner durch den Ursprung des Koordinatensystems
und schneidet die x-Achse an der Stelle x=3 mit der Steigung m= - 48.
10.) Der Graph einer ganzrationalen
Funktion f 5. Grades ist symmetrisch zum Ursprung des Koordinatensystems.
In N(0 / 0) ist die Steigung der Tangente an den Graphen 2 und im Punkt
W(-1 / 0) besitzt der Graph einen Wendepunkt.
Übungsaufgaben aus dem Bereich der Physik:
11.) Auf einer Teststrecke wurde bei trockener Fahrbahn ein Pkw aus verschiedenen Geschwindigkeiten abgebremst und die Länge des Bremswegs gemessen:
![]()
Welche ganzrationale Funktion f beschreibt den Zusammenhang
der Maßzahlen?
Lösen Sie mit DERIVE !
Zeichnen Sie den Graphen zu f im Graphikfenster von DERIVE
im Bereich [20; 100] !
Wie lang ist der Bremsweg bei 90 km/h ? Lösen Sie mit DERIVE !
12.) Der Benzinverbrauch eines Autos
hängt von seiner Geschwindigkeit ab.
Bei der Verbrauchsuntersuchung für einen Lieferwagen messen die Ingenieure
bei verschiedenen konstanten Geschwindigkeiten den Benzinverbrauch in
Liter für je 100 gefahrene Kilometer:
| Geschwindigkeit x km/h |
30
|
70
|
120
|
| Verbrauch in Liter je 100 km |
7,2
|
6,4
|
9,8
|
Aus der Erfahrung ist bekannt, dass die Abhängigkeit des Benzinverbrauchs von der Geschwindigkeit durch eine ganzrationale Funktion 2. Grades beschrieben werden kann.
a) Bestimmen Sie die Funktionsgleichung für die Verbrauchsfunktion
V mit DERIVE ( x bezeichnet die Geschwindigkeit, V(x) die Maßzahl
für den Verbrauch) !
Stellen Sie auch die Verbrauchskurve, d.h. den Graphen zu V, im Graphikfenster von DERIVE
dar. Dabei soll in der Zeichnung berücksichtigt werden, dass
der Lieferwagen eine Höchstgeschwindigkeit von 150 km/h hat.
b) Ermitteln Sie mit DERIVE die Geschwindigkeit des Lieferwagens, bei der der Benzinverbrauch am geringsten ist! Wie hoch ist dann der geringste Benzinverbrauch und wieviel Liter Benzin verbraucht der Lieferwagen bei Tempo 150 km/h auf je 100 gefahrenen Kilometer?
Übungsaufgaben aus dem Bereich der Biologie
13.) Viele natürliche Ressourcen wie z. B. Fisch-
oder Waldbestände erneuern sich von selbst. Waldbesitzer oder Fischzüchter
möchten aber einen möglichst großen Ertrag erwirtschaften.
Dabei ist darauf zu achten, dass sie nicht zu viel Holz schlagen oder
zu viele Fische der Zucht entnehmen.
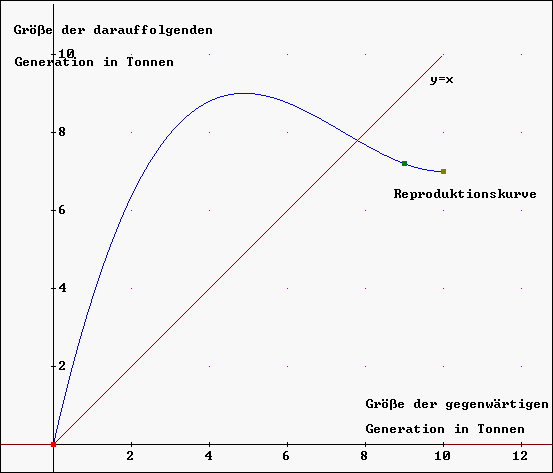
Unten ist nun eine sogenannte Reproduktionskurve einer Art abgebildet.
Sie ist der Graph einer Funktion f, die der Populationsgröße
der gegenwärtigen Generation die Populationsgröße der
darauffolgenden Generation zuordnet. Auch wenn diese Kurve von Art zu
Art variiert, so hat sie unter vernünftigen biologischen Annahmen
immer eine ähnliche Form wie die abgebildete Reproduktionskurve für
einen Fischbestand.
Bei einer wirtschaftlichen Nutzung des Fischbestands versucht der Züchter
nun, jährlich eine möglichst konstante Entnahme E zu tätigen.
Da die Fischpopulation in einem Jahr von x auf f(x) zunimmt, beträgt
dann der natürliche Zuwachs f(x) - x. Daher wird eine konstante Entnahme
E erreicht, wenn gilt: E = f(x) - x.
(a) Bestimmen Sie mit Hilfe von DERIVE die Gleichung der Reproduktionskurve f unter Beachtung folgender Tabelle ( f soll eine ganzrationale Funktion 3. Grades sein):
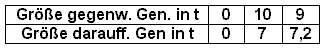
Beachte: Für 10 Tonnen liegt ein lokales Extremum vor!
(b) Bestimmen Sie mittels DERIVE das Maximum (in t) der Entnahme E, die der Züchter dem Bestand entnehmen darf ! Wie groß (in t) darf also die Population werden?
14.) Um die Bekämpfung von Schadinsekten zu optimieren, beobachtet man in gleichen Zeitintervallen (z. B. zwei Wochen) die Dichte des Befalls, indem man die Anzahl der Insekten pro dm2 großflächig auszählt und dann den Mittelwert bildet. Diese Werte trägt man dann in eine Tabelle ein:
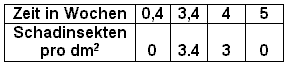
(a) Bestimmen Sie aus den Tabellenwerten mit Hilfe von
DERIVE die Gleichung einer ganzrationalen Funktion f 3. Grades,
die den zeitlichen Verlauf des Schadinsektenbefalls annähert!
Zeichnen Sie dann im Graphikfenster von DERIVE den Graphen zu f
im Bereich 0,4 £
x £ 5 !
(b) Zu welchem Zeitpunkt war im Beobachtungszeitraum
ein maximaler Befall mit Schadinsekten zu verzeichnen?
Lösen Sie mit DERIVE !
Übungsaufgaben aus dem Bereich der Medizin
15.)
Um die Wirkung von Medikamenten beurteilen zu
können, wäre es wünschenswert ihre Konzentration
im Organismus zu kennen. Da die Konzentration in den einzelnen
Organen jedoch nur schwer messbar ist, behilft man sich, indem
man die Konzentration eines Wirkstoffs im Blut oder im Urin misst.
Bei der Blutkonzentration handelt es sich genauer um die Konzentration
im Blutplasma (Plasmakonzentration). Unter Plasma versteht man das Blut
ohne seine korpuskulären Bestandteile, d.h. ohne rote oder weiße
Blutkörperchen und ohne Blutplättchen.
Hier soll nun die Plasmakonzentration von Iboprofen untersucht werden,
welches ein weit verbreitetes Schmerzmittel ist. Da bei diesem Wirkstoff
je nach chemischer Verbindung, in der es verabreicht wird, die
Konzentrationskurve (auch Plasmaspiegel genannt) stark variiert, ist die
Untersuchung hier von besonderem Interesse.
Die genaue Konzentration ist von Patient zu Patient verschieden. Daher
soll im Folgenden die durchschnittliche Plasmakonzentration bei Gabe von
400 mg Ibuprofen betrachtet werden.
(a) Bestimmen Sie die Funktionsgleichung mit Hilfe der untenstehenden Angaben!
| Stunden in h | 0 | 2 | 3 |
| Durchschnittliche Konzentration in mg/ml |
0 | 35 | 22 |
Nach zwei Stunden ist die höchste Konzentration erreicht.
Stellen Sie dazu die notwendigen Bedingungen auf und lösen
Sie das zugehörige lineare Gleichungs-
system von Hand und anschließend mit DERIVE !
Stellen Sie auch den Graphen zu f im Bereich 0 £ x £ 3,3 im
Graphikfenster von DERIVE dar!
Minimieren Sie dazu den Internet Browser (oben rechts, linker Button)
und rufen Sie das Programm
DERIVE auf ! Kehren Sie danach wieder in den Lehrgang zurück!
(b) Für den Einsatz eines Medikaments ist es von Interesse, wann nur noch die Hälfte der
Höchstkonzentration vorliegt. Man bezeichnet dies als (Plasma-)Halbwertzeit.
Berechnen Sie näherungsweise die Halbwertzeit von 400 mg Ibuprofen mittels DERIVE .
ANMERKUNG: Die Abnahme der Konzentration im Blutplasma kann in geeigneter Weise durch eine Exponentialfunktion dargestellt werden.
16.) In einer Versuchsreihe wird die fiebersenkende Wirkung von Ibuprofen untersucht. Vor dem Test am Menschen werden Versuche an Ratten durchgefürt. Bei einer Gabe von 5mg Ibuprofen pro kg Körpergewicht wurden folgende Werte ermittelt:
| Stunden in h | 0 | 1 | 2 | 4 |
| Veränderung der Rektaltemperatur in oC ab Startzeit |
0 | - 0,9 | - 1,2 | - 1,1 |
(a) Bestimmen Sie die Funktionsgleichung!
Stellen Sie dazu die notwendigen Bedingungen auf und lösen
Sie das zugehörige lineare Gleichungs-
system von Hand und anschließend mit DERIVE !
Stellen Sie auch den Graphen im Bereich 0 £ x £ 4 zu f im
Graphikfenster von DERIVE dar!
Minimieren Sie dazu den Internet Browser (oben rechts, linker Button)
und rufen Sie das Programm DERIVE auf ! Kehren Sie danach
wieder in den Lehrgang zurück!
(b) Zu welchem Zeitpunkt ist das Fieber am niedrigsten und wie groß ist die erreichte Fiebersenkung.
Übungsaufgaben aus dem Bereich der Wirtschaft
17.) (a) Bestimmen Sie die (Gesamt-)Kostenfunktion K eines Unternehmens in Abhängigkeit von der Produktionsmenge x, wobei K eine ganzrationale Funktion 3. Grades sein soll, die die folgende Wertetabelle erfüllt (ME = Mengeneinheiten, GE = Geldeinheiten):
![]()
Die fixen Kosten betragen betragen 81 GE, die Erlösfunktion E ist gegeben durch E(x) = 90x.
(b) Bestimmen Sie die Gewinnfunktion G und berechnen Sie mit DERIVE, für wieviele ME der Gewinn maximal wird!
(c) Zeichnen Sie im Graphikfenster von DERIVE die Graphen zur Kostenfunktion K, zur Erlösfunktion E und zur Gewinnfunktion G !
(d) Berechnen Sie die Nutzenschwelle und die Nutzengrenze
mit DERIVE !
18.) In einer landwirtschaftlichen Versuchsstation
wird auf mehreren Versuchsfeldern gleicher Qualität die Abhängigkeit
der Kartoffelerträge von der zugeführten Düngermenge untersucht.
Die Maßzahl des Ertrages wird mit E(x), die Maßzahl der Düngermenge
mit x bezeichnet. Es wird festgestellt, dass der Ertragsverlauf näherungsweise
durch eine ganzrationale Funktion 3. Grades dargestellt werden kann.
(a) Ermitteln Sie die Funktionsgleichung der Ertragsfunktion E aus folgenden Bedingungen: Ein ungedüngtes Feld liefert 40 Zentner Kartoffeln. Eine Düngung mit 10 kg Düngemittel steigert den Ertrag auf das Dreifache; gleichzeitig erreicht man dadurch den maximalen Ertrag. Falls kein Dünger verwendet wird, nimmt man eine waagerechte Tangente an (d. h. der Grenzertrag ist gleich Null) !
(b) Bei welcher Düngermenge (in kg) ist der größte Ertragszuwachs zu erwarten? Lösen Sie mit DERIVE und stellen Sie den Graphen der Ertragsfunktion E im Bereich 0 £ x £ 11 dar!
Übungsaufgaben aus dem Bereich des Alltags
19.) Beim Bau einer Gokart-Bahn sollen zwei parallele gerade Teilstücke der Fahrbahn ( [AB] und [CD] ; siehe untenstehendes Schaubild) mittels einer s-förmige Kurve, die zwischen den beiden Fahrbahnteilen dem Graphen einer ganzrationalen Funktion 3. Grades entspricht, ohne Knick in B und C verbunden werden:
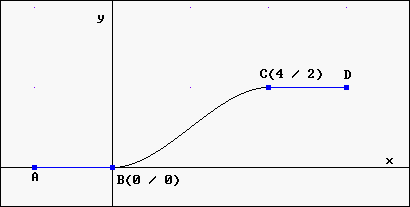
Bestimmen Sie die Gleichung
dieser ganzrationalen Funktion mit DERIVE !
20.) Um die Ortschaft D, die an der geraden Straße durch A(0 / 4) und B(4 / 0) liegt, wird eine Umgehungsstraße gebaut. Diese soll in A und B tangential in die alte Straße münden und durch den Punkt C(2 / 1) gehen (siehe Bild, Einheit: 1 km ):
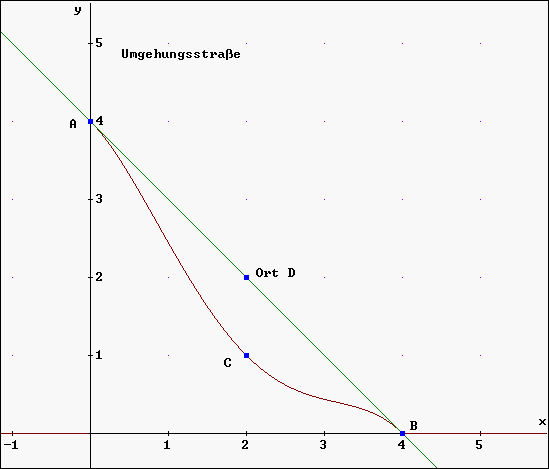
Bestimmen Sie mittels DERIVE eine ganzrationale Funktion f 4. Grades, die den obigen Bedingungen entspricht und zeichnen Sie den Graphen zu f im Bereich 0 £ x £ 4 im Graphikfenster von DERIVE ! Zeichnen Sie auch die Gerade durch A und B ein!
|
|
|