Seite 18 Thema: Einführung in die Integralrechnung

Diese Besonderheit der Integralrechnung sollen wir uns merken:

Bei der Integralrechnung ist zu beachten, dass die Flächeninhalte orientiert, d.h. vorzeichenbehaftet sind. Hierbei sind ....

a.) ... Flächeninhalte oberhalb der x-Achse mit einem positiven Vorzeichen versehen.

b.) ...Flächeninhalte unterhalb der x- Achse mit einem negativen Vorzeichen versehen.

Bei Programmen werden daher immer orientierte Flächeninhalte UND absolute Flächeninhalte ausgewiesen.

Wir werden zunächst nur absolute Flächeninhalte berechnen. Hier müssen wir immer die Beträge addieren.

Bevor wir das tun können, muss aber immer zunächst geklärt werden, wo die Flächenanteile ihr Vorzeichen wechseln. Diese Punkte sind die bereits immer wieder berechneten Nullstellen sind.

Folgerungen:
Wenn die Fläche unter einem Graphen in einem vorgegebenen Intervall I = [a; b] zu berechnen ist, muss zunächst geklärt werden, ob die Nullstellen im Intervall liegen. Ist das der Fall, muss die Flächenberechnung "geteilt" werden.
Wir berechnen dann die Flächen unter dem Graphen für die Teilintervalle I₁= [a; x_N] und I₂ = [x_N; b].

In unserem Beispiel müssen wir wie folgt vorgehen:

-------

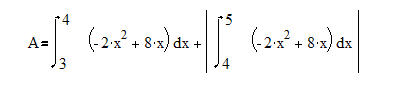
Berechne selbst!!!

-------

Wenden wir jetzt uns den Aufgaben des Fachbuches zu.

Wer weitere Hilfen benötigt sollte sich die Seiten des Kollegen Brinkmann (Duisburg) ansehen. (Link)

Auch dort gibt es viele Übungsaufgaben mit Lösungen.

-> weiter zur nächsten Seite oder zurück