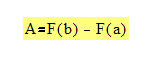
Seite 15 Thema: Einführung in die Integralrechnung

Wir wollen nun noch die zugehörigen Schreibweisen kennen lernen. Die Integralrechnung hat eine "eigene Form" entwickelt, die langfristig der Übersichtlichkeit dient.

Zur Erinnerung:

--------

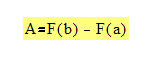
Wir wollen nun noch die zugehörigen Schreibweisen kennen lernen. Die Integralrechnung hat eine "eigene Form" entwickelt, die langfristig der Übersichtlichkeit dient.

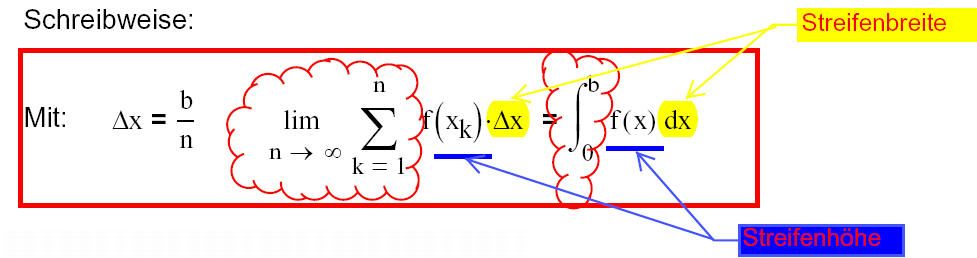
Wir erinnern uns: Bei der Flächenberechnung haben wir zunächst nährerungsweise die Flächen von Rechtecke (OS bzw. US) addiert. Die Genauigkeit konnte verbessert werden, indem wir die Anzahl (n) der "Rechteckstreifen" erhöht haben. Gleichzeitig wurde dadurch die "Streifenbreite" verkleinert. "Ideal" wurde das Ergebnis, wenn wir die Anzahl auf "unendlich" (∞)erhöhen. Gleichzeitig wurde dann die "Streifenbreite" "unendlich klein". Mathematisch wird dieses Vorgehen mit der Grenzwertrechnung ermöglicht. Für die Summenbildung verwendet der Mathematiker auch ein eigenes Symbol (∑). Halten wir fest:

Die Erhöhung der Streifenzahl wird umgesetzt mit:

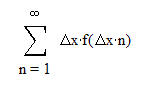weiter =Streifenfläche (Umbenennung von n und m)

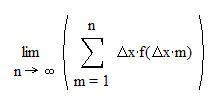Die Streifenbreite Δx wird, wenn diese unendlich klein, also fast 0 wird zu dx.

Mit Hilfe diese Schreibweisen erhalten wir:

Unkommentiert reduziert sich diese Schreibweise auf:

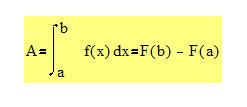
Mit dieser Schreibweise wollen wir nun exemplarische eine bereits bekannte Aufgabe lösen!

------------

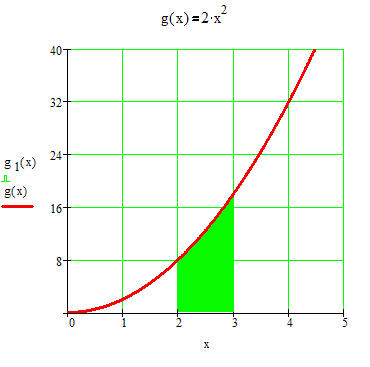
Mit Hilfe der Integrationsregeln bestimmen wir die zu g(x) = 2x² zugehörige Flächenfunktion G(x):
-----------

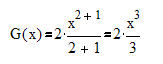
Nun schreiben wir:

Üben Sie nun selbst!!!!!!

-> weiter zur nächsten Seite oder zurück