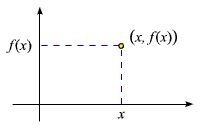|
Ein Beispiel für einen Zusammenhang zwischen Größen ist
die Abhängigkeit der Höhe der Telefonrechnung von der Gesprächszeit.
Sie kann in Worten beschrieben oder durch eine Formel ausgedrückt
werden.
Aufgabe: Ein Handybetreiber bietet folgenden Tarif an: Die monatliche
Grundgebühr beträgt 15 €. Für 1 Minute telefonieren
in alle Netze Österreichs werden 0,06 € verrechnet. Die
Abrechnung erfolgt minutengenau (d.h. für eine angebrochene Minute
wird der volle Preis für 1 Minute verrechnet). Um schnell ermitteln
zu können, wie hoch die Rechnung für eine gegebene Gesprächszeit
ist, ist es praktisch, eine Formel dafür zur Hand zu haben:
- Berechne die Höhe der monatlichen Handyrechnung für eine
Gesprächszeit von 1 min!
- Berechne die Höhe der monatlichen Handyrechnung für eine
Gesprächszeit von 2 min!
- Berechne die Höhe der monatlichen Handyrechnung, wenn die Gesprächszeit
(in Minuten) mit t
bezeichnet wird!
Tipp: Trage die Geldbeträge in die folgende Tabelle ein!
Fällt dir eine Gesetzmäßigkeit auf, die es dir erlaubt,
auch die letzte Zeile auszufüllen?
| Gesprächszeit in Minuten |
Höhe der Handyrechnung in € |
| 0 |
|
| 1 |
|
| 2 |
|
| 3 |
|
| 10 |
|
| 20 |
|
| 50 |
|
| t |
|
Benutze dabei ein Werkzeug deiner Wahl, beispielsweise:
| |
 Derive
(Speichern und Auswerten einer Formel) Derive
(Speichern und Auswerten einer Formel) |
|
In der vorigen Aufgabe hast du die Abhängigkeit einer Größe
(Höhe der Handy-Rechnung) von einer anderen (Gesprächszeit) betrachtet
und durch eine Formel beschrieben. Nun wollen wir uns weiteren Darstellungsformen
von Abhängigkeiten zuwenden.
|
Die Abhängigkeit der Höhe der Telefonrechnung von der Gesprächszeit
kann in Form einer Tabelle dargestellt werden.
Aufgabe: In der vorhergehenden Aufgabe hast du eine Formel für
die Handyrechnung aufgestellt. Sie beschreibt, wie die Höhe der Rechnung
von der Gesprächszeit abhängt.
An der Hotline des Handyanbieters sitzt ein Mitarbeiter, der Formeln
nicht ausstehen kann! Dennoch muss er vielen AnruferInnen mitteilen, wie
hoch ihre Rechnung sein wird, wenn sie soundsoviel telefonieren. Er bevorzugt
die Verwendung einer Tabelle, in der alle für ihn relevanten Zahlen
stehen.
Erstelle mit einem Werkzeug deiner Wahl eine Tabelle für den Betreuer
der Hotline! Sie soll die Höhe der Rechnung für alle Gesprächszeiten
bis 200 Minuten enthalten:
| Gesprächszeit in Minuten |
Höhe der Handyrechnung in € |
| 0 |
|
| 1 |
|
| 2 |
|
| 3 |
|
| ... |
|
| 200 |
|
Benutze dabei ein Werkzeug deiner Wahl, beispielsweise:
Beachte: Die idealen Werkzeuge zum Erstellen und Manipulieren von Tabellen
sind, wie schon der Name sagt, die Tabellenkalkulationsprogramme
(z.B. Excel). CAS-Rechner wie Voyage und TI 92 bieten zwar gewisse
Möglichkeiten in dieser Richtung, sind aber ein bisschen schwerfällig,
insbesondere wenn es um Tabellen mit vielen Einträgen geht.
|
In der Mathematik wird eine Tabelle, wie du sie in der vorigen Aufgabe erstellt
hast, als Wertetabelle bezeichnet. In der linken Spalte stehen die Gesprächszeiten,
und zu jeder Gesprächszeit t
ist in der rechten Spalte der entsprechende Rechnungsbetrag H(t)
verzeichnet.
|
Mit Hilfe einer Tabelle lassen sich verschiedene Fragen schnell beantworten.
Aufgabe: In der vorhergehenden Aufgabe hast du eine Wertetabelle
erstellt, die der Betreuer der Handy-Hotline benutzen kann, um Fragen
zu den Telefonkosten zu beantworten. Umgegend erhält er einige Anrufe.
Nimm die Tabelle zur Hand und hilf ihm, die richtigen Auskünfte zu
erteilen!
| Anfrage |
Antwort |
| (1) Sylvia möchte wissen, wie hoch ihre Rechnung
ist, wenn sie pro Monat genau eine Stunde lang telefoniert. |
|
| (2) Fritz möchte wissen, wie hoch seine Rechnung ist, wenn
seine monatliche Gesprächszeit eine Stunde und 15 Minuten
beträgt. |
|
| (3) Sabine erhält im Monat 30€ Taschengeld und will davon
höchstens 21 € für die Handyrechnung ausgeben.
Sie möchte wissen, wie viele Minuten sie pro Monat höchstens
mit ihrem Handy telefonieren darf. |
|
| (4) Max ruft bei der Hotline an und verwickelt den Betreuer in eine
Diskussion. Er sagt: "Wenn ich doppelt so viel telephoniere als
im Vormonat, ist meine Rechnung doppelt so hoch!" Hat er recht? |
|
|
In den bisherigen Aufgaben sind nur diskrete Zahlenwerte (ganzzahlige
Minuten- und Eurobeträge) vorgekommen. Abhängigkeiten können
aber auch für kontinuierlichen Größen, die beliebige
reelle Zahlenwerte annehmen können, auftreten.
|
Ein Beispiel für eine Abhängigkeit zwischen geometrischen Größen
entsteht beim Basteln einer Schachtel.
Aufgabe: Aus einem quadratischen Stück Papier (Seitenlänge
6) soll eine Schachtel hergestellt werden. Dazu werden bei den Ecken vier
kleinere (gleich große) Quadrate herausgeschnitten und das verbleibende
Stück Pappe zu einer Schachtel (ohne Deckel) aufgeklappt. Betrachte
dazu die Flash-Animation
 Aufgabenstellung Aufgabenstellung
Wir werden uns in den nächsten Lernschritten damit beschäftigen,
wie die Schachtel dimensioniert werden muss, damit ihr Volumen möglichst
groß ist. Dazu fragen wir zunächst, wie groß ihr Volumen
überhaupt ist! Das hängt natürlich davon ab, wie groß
die Quadrate sind, die zunächst herausgeschnitten wurden.
- Berechne das Volumen der Schachtel, wenn die Seitenlänge der
herausgeschnittenen Quadrate 1 beträgt!
- Berechne das Volumen der Schachtel, wenn die Seitenlänge der
herausgeschnittenen Quadrate 2 beträgt!
- Ermittle eine Formel für das Volumen der Schachtel, wenn die
Seitenlänge der herausgeschnittenen Quadrate (wie in der Animation)
mit x
bezeichnet wird!
|
Auch diese Form der Abhängigkeit einer Größe von einer anderen
kann in Tabellenform dargestellt werden. Allerdings haben wir hier die Freiheit,
zu wählen, wie viele Eintragungen eine solche Tabelle enthalten
soll.
|
Die Abhängigkeit einer reellen Größe von einer anderen
kann in Form einer Tabelle dargestellt werden. Allerdings können
wir nicht alle reellen Zahlen aufzählen und müssen uns daher
auf einzelne ausgewählte Werte beschränken. Dementsprechend
können aus einer Abhängigkeit verschiedene Tabellen (die sich
z.B. durch die Schrittweite unterscheiden) gewonnen werden.
Aufgabe: In der vorhergehenden Aufgabe wurde das Volumen der Schachtel
in Abhängigkeit von x,
der Seitenlänge der herausgeschnittenen Quadrate, berechnet. Was
nützt uns eine solche Formel? Wir können die durch sie beschriebene
Abhängigkeit auf verschiedene Weisen darstellen. Eine Darstellungsform
ist die Wertetabelle, d.h. eine Auflistung von ausgewählten
Werten von x
mit den zugehörigen Werten von V(x).
Eine einfache Wertetabelle sieht so aus:
Sie besagt: Haben die herausgeschnittenen Quadrate die Seitenlänge
1, so ist das Volumen der Schachtel 16. Haben die herausgeschnittenen
Quadrate die Seitenlänge 2, so ist das Volumen der Schachtel 8.
Wir wollen es aber jetzt genauer wissen! Erstelle aus der Formel V(x)
= (6 - 2x)2x
für das Schachtelvolumen
- eine Wertetabelle für Werte von x
zwischen 0 und 3 mit einer Schrittweite von 0.3, und
- eine Wertetabelle für Werte von x
zwischen 0 und 3 mit einer Schrittweite von 0.1!
Benutze dabei ein Werkzeug deiner Wahl, beispielsweise den CAS-Rechner
Voyage/TI 92,
Derive
oder Tabellenkalkulation.
Beachte: Die idealen Werkzeuge zum Erstellen und Manipulieren von Tabellen
sind, wie schon der Name sagt, die Tabellenkalkulationsprogramme
(z.B. Excel). CAS-Rechner wie Voyage und TI 92 bieten zwar gewisse
Möglichkeiten in dieser Richtung, sind aber ein bisschen schwerfällig,
insbesondere wenn es um Tabellen mit vielen Einträgen und um Vergleiche
mehrerer Tabellen geht.
Wenn du die Tabellen fertiggestellt hast, betrachte die in ihnen stehenden
Zahlen. Beantworte die folgenden Fragen:
- Wie ist x
zu wählen, damit das Volumen der Schachtel möglichst groß
wird? Wie groß ist dieses maximale Volumen?
- Verfolge und beschreibe in eigenen Worten, wie sich die Werte von
V
mit wachsendem x
verändern. Erkläre ihr Verhalten! Warum ist das Volumen
zunächst klein, wächst dann an und wird schließlich
wieder kleiner?
- Wie genau ist deine Antwort auf die Frage 1?
|
Nun wollen wir genau definieren, wie Abhängigkeiten in der Mathematik
beschrieben werden.
|
In den bisherigen Aufgaben ist es darum gegangen, Abhängigkeiten
- durch eine Formel auszudrücken und
- in Tabellenform wiederzugeben
Was haben das Handybeispiel und das Schachtelbeispiel gemeinsam? In beiden
Fällen haben wir Vorschriften betrachtet, die es gestatten,
|
|
 |
ein anderes, davon
abhängiges Objekt |
|
| |
|
|
| z.B. die Länge der Quadratseite x |
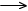 |
das Schachtelvolumen V(x) |
zuzuordnen. Diese Idee der Zuordnung ist in der Mathematik sehr
wichtig. Dabei können wir an ganz unterschiedliche Objekte (wie beispielsweise
natürliche Zahlen oder reelle Zahlen) denken.
Wir wollen nun etwas genauer formulieren, wie die Idee der Zuordnung
für die Mathematik nutzbar gemacht werden kann. Dazu müssen
wir - wie es dem Genauigkeitsanspruch der Mathematik
entspricht - für jede konkrete Zuordnung
festlegen, um welche Objekte es sich dabei handelt. Wir fassen alle möglichen
"gegebenen Objekte" in einer Menge A
zusammen und stellen uns vor, dass alle möglichen "abhängigen
Objekte" in einer Menge B
liegen. So gelangen wir zur Definition des Funktionsbegriffs, wie
er in der Mathematik seit mehr als 100 Jahren verwendet wird:
| Definition: Seien A
und B
zwei Mengen. Eine Funktion von A
nach B
ist eine Vorschrift, die jedem Element der Menge A
ein (d.h. genau ein) Element der Menge B
zuweist. |
Bezeichnungen:
- Die Menge A
nennen wir Definitionsmenge, die Menge B
heißt Zielmenge.
- Wie andere mathematische Objekte auch werden Funktionen mit Symbolen
(in der Regel mit Buchstaben) bezeichnet. Bezeichnen wir eine Funktion
von A
nach B
mit dem Buchstaben f,
so schreiben wir dafür auch
f : A
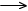 B B
(ausgesprochen: "f
ist eine Funktion von A
nach B").
- Wir sagen auch: Jedes x
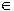 A wird von
der Funktion f
auf ein Element von B
abgebildet. Dieses Element von B
schreiben wir als A wird von
der Funktion f
auf ein Element von B
abgebildet. Dieses Element von B
schreiben wir als
f(x).
Funktionen werden manchmal auch Abbildungen genannt.
- Lässt sich durch einen Term (d.h. durch eine Formel) angeben,
wie f(x)
aus x
ermittelt wird, so sprechen wir von einer "Termdarstellung
der Funktion f".
So ist beispielsweise durch die Termdarstellung
f(x)
= x2
jene Funktion definiert, die jedem Element der Definitionsmenge sein
Quadrat zuordnet. Die Aussage f(x)
= x2 wird auch als Funktionsgleichung
bezeichnet. Eine andere Schreibweise dafür ist
f : x
 x2. x2.
Eine Termdarstellung ist eine durch einen Term ausgedrückte Zuordnungsvorschrift.
Die meisten elektronischen Rechenwerkzeuge gestatten es, eine Funktion,
d.h. eine Zuordnungsvorschrift einzugeben, um sie später bei
Bedarf anwenden zu können.
|
In vielen Anwendung der Mathematik auf reale Situationen kommen Abhängigkeiten
vor, die durch Formeln beschrieben werden. Beim Aufstellen eines mathematisch
strengen Modells einer solchen Situation ist es oft nötig, von Formeln
zu Funktionen überzugehen.
Die folgenden Bemerkungen stellen dar worauf es dabei ankommt. Sie werden dir
bei den nachfolgenden Aufgaben helfen.
|
Funktionen beschreiben Abhängigkeiten zwischen Größen.
Wenn eine Größe (z.B. der Flächeninhalt eines Quadrats)
von einer anderen Größe (z.B. die Seitenlänge) abhängt,
so kann diese Abhängigkeit durch eine Funktion beschrieben werden.
Bezeichnen wir den Flächeninhalt mit F
und die Seitenlänge mit a,
so ist F
= a2. Das ist zunächst nur eine "Formel".
Motiviert durch diese Formel können wir eine Funktion
definieren:
- Zuordnungsvorschrift (Termdarstellung):
F(a)
= a2.
Das bedeutet: Der Flächeninhalt wird gewonnen, indem die Seitenlänge
quadriert wird.
- Angabe von Definitions- und Zielmenge:
Definitionsmenge =
Menge R+
aller positiven reellen Zahlen
Zielmenge =
Menge R
aller reellen Zahlen
Wir können das in Kurzform als
F
: R+
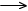 R
R
anschreiben. Das bedeutet: Jeder positiven reellen Zahl (der Seitenlänge)
wird eine reelle Zahl (der Flächeninhalt) zugeordnet.
Beachte, dass der Begriff der "Funktion" schärfer als
jener der "Formel" ist!
Der Name der abhängigen Größe wird oft (wie auch im obigen
Beispiel) als Name der Funktion verwendet. Durch die Schreibweise F(a)
= a2 wird ausgedrückt, wie F
von a
abhängt.
| Die Größe |
nennen wir... |
| a |
...die unabhängige Variable
(das Argument) - sie kann
innerhalb der Definitionsmenge
frei gewählt werden. |
| F
bzw. F(a) |
...die abhängige Variable
(den Funktionswert) - für
einen gegebenen Wert der
unabhängigen Variable ist sie
ein Element der Zielmenge. |
Achtung: Der Schritt von einer Formel zu einer Funktion ist nicht immer
eindeutig. So könnte man durchaus auch bei der Quadratfläche
den Grenzfall a
= 0 zulassen und als Definitionsmenge R+0
= { x 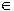 R | x R | x
 0}
wählen. Als Zielmenge könnte man statt R
genauso gut R+0
(oder, wenn die Definitionsmenge R+
ist, ebenfalls R+)
angeben.
0}
wählen. Als Zielmenge könnte man statt R
genauso gut R+0
(oder, wenn die Definitionsmenge R+
ist, ebenfalls R+)
angeben.
|
In den folgenden beiden Aufgaben sollst du die obigen Definitionen anwenden
und Abhängigkeiten als Funktionen formulieren.
|
In dieser Aufgabe sollst du den bereits bekannten Zusammenhang zwischen
der Gesprächsdauer und der Höhe der Telefonrechnung als Funktion
formulieren.
Aufgabe: Die Höhe der Handyrechnung in Abhängigkeit von
der Gesprächsdauer kann durch die Formel
H(t)
= 0,06
t + 15
beschrieben werden.
- Welche Werte von t
sind zulässig, welche nicht?
- Welche Möglichkeiten hast du, H
im strengen mathematischen Sinn als Funktion
H:
A 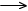 B B
zu definieren? Gib die Definitions- und Zielmenge an!
- Gib die abhängige und die unabhängige Variable an!
- Gib die Funktionswerte für t
= 0, 15, 43 und 167 an!
- Für welche Argumente ergibt sich ein Funktionswert von 16,5;
18,84; 26,1?
|
|
In dieser Aufgabe sollst du einen bereits bekannten Zusammenhang zwischen
geometrischen Größen als Funktion formulieren.
Aufgabe: Im Schachtelbeispiel tritt die Formel
V(x)
= (6 - 2x)2 x
auf.
- Welche Werte von x
sind im Rahmen dieses Beispiels (sinnvollerweise) zulässig, welche
nicht?
- Welche Möglichkeiten hast du, V
im strengen mathematischen Sinn als Funktion
V:
A 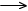 B B
zu definieren? (Tipp: Setze die Werte x
= 4, x
= 10 und x
= -1 ein und berechne jeweils
V(x).
Was bedeuten die Resultate?) Gib Definitions- und Zielmenge an!
- Gib die Funktionswerte für x
= 0,5; 1,3 und 2,4 an!
- Für welche Argumente ergibt sich ein Funktionswert von 6,272;
12,544 bzw. 0,972?
|
Wir kommen nun zu einer sehr nützlichen Darstellungsform für Funktionen.
|
Abhängigkeiten zwischen Größen können auf grafische
Weise dargestellt werden. Auch diese Darstellungsform kann mathematisch
genauer gefasst werden:
Definition: Der Graph einer Funktion
f
: A 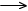 B ist die Menge aller Paare (x,
f(x)), d.h. die Menge
B ist die Menge aller Paare (x,
f(x)), d.h. die Menge |
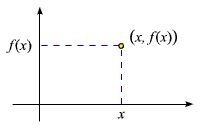 |
{
(x, f(x) | x 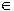 A } .
A } .
|
| Falls es sich bei A
und B
um Zahlenmengen handelt, kann jedes Paar (x,
f(x)), wie in der Skizze gezeigt,
als Punkt in der Zeichenebene dargestellt werden. In diesem
Fall ist der Graph eine Teilmenge der Zeichenebene. (Für
viele Funktionen, die du kennen lernen wirst, ist er eine Kurve.) |
|
Um Funktionen grafisch darzustellen, kannst du eine Vielzahl elektronischer
Werkzeuge benutzen. Einige davon kannst du in den folgenden Aufgaben kennen
lernen.
|
Die graphische Darstellung von Funktionen wollen wir nun ein bisschen üben.
|
Mit Hilfe der grafischen Darstellung einer Funktion können manche
Aufgabenstellungen ganz bequem gelöst werden.
Aufgabe: In der Aufgabe "Schachtelbeispiel (2")
hast du zwei Wertetabellen für den Zusammenhang zwischen V
und x
erstellt.
- Stelle den Zusammenhang grafisch auf Papier dar!
(Tipp: Jede Zeile in einer Wertetabelle wird durch einen Punkt in der
Zeichenebene dargestellt. Wähle einige beliebige Zeilen einer Wertetabelle
aus und zeichne die entsprechenden Punkte in der Ebene ein! Der Graph
ist die Menge aller Punkte, die du auf diese Weise einzeichnen
könntest: er ist eine Kurve).
- Stelle den Zusammenhang mit einem geeigneten Werkzeug grafisch dar!
Für die zweite Aufgabenstellung benutze ein Werkzeug deiner Wahl,
beispielsweise
oder:
Nun kehre zur ursprünglichen Fragestellung zurück und beantworte
mit Hilfe des erstellten Graphen die Fragen:
- Wie ist x
zu wählen, damit das Volumen der Schachtel möglichst groß
wird?
- Wie groß ist dieses maximale Volumen?
- Wie genau kannst du diese Fragen mit Hilfe der Grafik beantworten?
- Vergleiche deine Antwort mit jenen, die du in der Aufgabe "Schachtelbeispiel
(2)" aus deinen Wertetabellen gewonnen hast!
|
|
Auch der Zusammenhang zwischen der Gesprächszeit und der Höhe
der Telefonrechnung kann grafisch dargestellt werden.
Aufgabe: Erinnere dich an die Wertetabelle für den Betreuer
der Handy-Hotline (Handybeispiel (2))! Sie beschreibt, wie die Höhe
H der
Handy-Rechnung von der Gesprächszeit t abhängt. Stelle die ersten
zehn Zahlenpaare grafisch auf Papier dar!
Stelle diese Abhängigkeit (bis zu einer sinnvollen Obergrenze für
t)
grafisch dar! (Der Graph ist in diesem Beispiel eine endliche Menge von
Punkten in der Zeichenebene, ein so genannter Punktgraph). Verwende
dabei ein Werkzeug deiner Wahl, beispielsweise:
Unser Hotline-Betreuer bekommt einen neuerlichen Anruf: Irene möchte
im Monat höchstens 20 € fürs Telefonieren ausgeben.
Wie viele Minuten darf sie dann telefonieren?
- Benutze zuerst die von dir erstellte Grafik, um diese Frage zu beantworten!
- Danach benutze die von dir erstellte Wertetabelle, um die Frage zu
beantworten!
Sind die beiden Antworten gleich? (Und sind sie gleich genau?) Welche
Methode fällt dir leichter?
|
Die folgenden Beispiele dienen zur Wiederholung, Anwendung und Vertiefung des
bisher Gelernten.
|
Aufgabe: An einer Straße wird die Zeit, die vorbeifahrende
Autos benötigen, um eine gekennzeichnete Strecke von 100 Metern
zu durchfahren, gemessen. Wird die Zeitspanne t
(in Sekunden) gemessen, so ergibt sich daraus eine Geschwindigkeit von
-
Benutze ein Tool deiner Wahl, um die Zuordnung t
 v(t) v(t)
grafisch darzustellen!
-
Erstelle eine Wertetabelle!
-
Definiere v
als Funktion v:
A 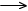 B B!
Begründe deine Wahl der Definitionsmenge A
und der Zielmenge B!
-
Beschreibe in eigenen Worten, wie sich v
für kleine und große t
verhält! Wie zeigt sich dieses Verhalten an der Lage und Form
des Graphen?
|
|
Aufgabe: Von einem rechtwinkeligen Dreieck mit Hypotenuse 1 ist
eine Kathete a
gegeben.
- Drücke die andere Kathete b
durch a
aus!
- Benutze ein Tool deiner Wahl, um die Zuordnung a
 b(a)
grafisch darzustellen! b(a)
grafisch darzustellen!
- Erstelle eine Wertemenge mit Schrittweite 0,1!
- Formuliere die Zuordnung als Funktion b:
A
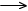 B!
Begründe deine Wahl der Definitionsmenge A
und der Zielmenge B! B!
Begründe deine Wahl der Definitionsmenge A
und der Zielmenge B!
- Wie verhält sich der Funktionswert, wenn a
nahe bei 1 liegt? Wie zeigt sich dieses Verhalten an der Lage und Form
des Graphen?
|
|
Aufgabe: Von einem Eisenbahnzug wird durch das automatische Sicherheitssystem
jede Minute die Position (in km vom Abfahrtbahnhof) ermittelt und aufgezeichnet:
Vergangene Zeit
(ab Abfahrt)
in Minuten |
Position (Entfernung
vom Abfahrtsbahnhof)
in Kilometern |
| 1 |
0,32 |
| 2 |
0,67 |
| 3 |
1,12 |
| 4 |
1,67 |
| 5 |
2,32 |
| 6 |
3,07 |
| 7 |
3,92 |
| 8 |
4,87 |
| 9 |
5,92 |
| 10 |
6,67 |
| 11 |
7,07 |
| 12 |
7,40 |
| 13 |
7,73 |
| 14 |
8,08 |
| 15 |
8,53 |
| 16 |
9,08 |
| 17 |
9,73 |
| 18 |
10,48 |
| 19 |
11,33 |
| 20 |
12,28 |
| 21 |
13,33 |
| 22 |
14,48 |
| 23 |
15,68 |
| 24 |
16,93 |
| 25 |
18,23 |
Betrachte die Zahlen in der Tabelle! Wie ist die Fahrt verlaufen? Kannst
du herausfinden, wo auf der Strecke sich eine Baustelle befindet, die
zum Langsamfahren zwingt?
Tipp: Die Zahlen der Tabelle nacheinander durchzugehen und zu
vergleichen, ist ein bisschen mühsam. Den schnellsten Überblick
über den Verlauf der Fahrt erhältst du mit Hilfe einer grafischen
Darstellung. Stelle den durch die Tabelle gegebenen Zusammenhang zwischen
der vergangenen Zeit und der erreichten Position des Zuges mit einem geeigneten
Werkzeug grafisch dar! Falls du Excel verwendest, kannst du die Tabelle
direkt in ein Arbeitsblatt kopieren. Falls du einen CAS-Rechner verwendest:
| |
 Voyage/TI
92 (Eine Tabelle im DataMatrix-Editor grafisch darstellen) Voyage/TI
92 (Eine Tabelle im DataMatrix-Editor grafisch darstellen) |
Kannst du anhand der Grafik nun leichter erkennen, wo sich die Baustelle
befindet?
|
- Aufgabe: Für eine bestimmte PKW-Marke lässt sich
der Bremsweg B
(in Metern) bei einer Geschwindigkeit v
(in km/h) in einer bestimmten Bremssituation durch folgenden Term darstellen:
B(v)
= 0,00856 v2.
- Formuliere diese Abhängigkeit als Funktion (d.h. wähle Definitions-
und Zielmenge)!
- Stelle die Funktion mit einem geeigneten Werkzeug grafisch dar!
- Beschreibe das Verhalten des Bremsweges in Abhängigkeit von der
Geschwindigkeit in deinen eigenen Worten!
- Zeige dass B(30)
= 7,704 gilt. Was bedeutet diese Aussage?
- Lies aus dem Graphen folgende Werte ab: Wie lang ist der Bremsweg
bei einer Geschwindigkeit von 25 km/h; 72 km/h; 104 km/h;
143 km/h?
Kontrolliere die abgelesenen Werte durch Einsetzen in die Funktionsgleichung!
- Bei welcher Geschwindigkeit ergibt sich ein Bremsweg von ca. 1 m;
35 m; 74 m; 138 m?
Kontrolliere die abgelesenen Werte durch Einsetzen in die Funktionsgleichung!
|
In der folgenden Aufgabe kannst du den Graphen einer Funktion auf interaktive
Weise selbst bestimmen:
|
Aufgabe: Rufe die interaktive Animation
 Temperaturkurve Temperaturkurve
(aus der Galerie
von mathe online)
auf! Mit Hilfe dieser interaktiven Animation kannst du einen
zeitlichen Temperaturverlauf bestimmen und mitverfolgen, wie die grafische
Darstellung zustande kommt. Bearbeite die in der Animationen eingebauten
Aufgabenstellungen!
|
Es gibt - neben den bereits gelernten -
noch weitere Möglichkeiten, Abhängigkeiten darzustellen. Die folgende
Lernhilfe kann dir dabei helfen, den Begriff der Funktion besser zu verstehen:
|
Aufgabe: Rufe das Applet
 Funktionale
Abhängigkeiten verstehen Funktionale
Abhängigkeiten verstehen
(aus der Galerie
von mathe online)
auf! Es zeigt eine weitere Darstellungsmöglichkeit
für funktionale Abhängigkeiten. Mache dich mit der Funktionsweise
dieses Werkzeugs vertraut! Studiere mit seiner Hilfe die Funktion
y(x)
= x2
- 5x
+ 6.
Für welche Werte von x
ist y(x)
= 0? (Damit hast du die Gleichung x2
- 5x
+ 6 = 0
gelöst!)
Mit diesem Tool kannst du auch das Schachtelbeispiel ein letztes Mal behandeln.
Beantworte mit seiner Hilfe die Frage, für welches x
das Volumen der Schachtel maximal ist!
|
Nun hast du die Gelegenheit, alles, was du bisher gelernt hast, noch einmal
anzuwenden:
|
Zum Abschluss eine Verallgemeinerung des Schachtelbeispiels, in dem nicht
von einem quadratischen, sondern von einem rechteckigen Stück Papier
ausgegangen wird.
Aufgabe: Aus einem rechteckigen Stück Papier (Seitenlängen
8 und 10) soll eine Schachtel hergestellt werden. Dazu werden bei den
Ecken vier kleinere (gleich große) Quadrate herausgeschnitten und
das verbleibende Stück Pappe zu einer Schachtel (ohne Deckel) aufgeklappt.
- Ermittle eine Formel für das Volumen der Schachtel, wenn die
Seitenlänge der herausgeschnittenen Quadrate (wie in der Animation)
mit x
bezeichnet wird!
- Erzeuge mit einem Werkzeug deiner Wahl eine Wertetabelle für
diese Abhängigkeit!
- Stelle diese Abhängigkeit mit einem Werkzeug deiner Wahl grafisch
dar!
- Formuliere diese Abhängigkeit im mathematisch strengen Sinn als
Funktion (d.h. wähle Definitions- und Zielmenge)!
- Benutze die Wertetabelle und/oder den Graphen, um herauszufinden,
wie x
gewählt werden muss, damit das Volumen der Schachtel möglichst
groß wird!
|
Überprüfe nun anhand eines interaktiven Tests, wie gut du dich mit
dem Begriff des Funktionsgraphen vertraut gemacht hast:
|
Aufgabe: Rufe den interaktiven Test
 Graph
oder nicht Graph Graph
oder nicht Graph
(aus den Interaktiven
Tests von mathe
online,
steht nur online zur Verfügung)
auf! Welche der Kurven stellen einen Funktionsgraphen dar?
Falls dir dieser Test schwer fällt, wiederhole den genauen Wortlaut
der Definition des Funktionsbegriffs: Jedem Element der Menge A
wird genau ein Element der Menge B
zugeordnet.
|
Die letzte Aufgabe ist besonders wichtig:
|
Aufgabe: Verfasse eine in deinen eigenen Worten formulierte Zusammenfassung
des Gelernten! Was erschien dir besonders wichtig? Was hast du gut, was
weniger gut verstanden? Bleiben offene Fragen?
Hebe deine Zusammenfassung gut auf!
|

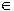 A wird von
der Funktion f
auf ein Element von B
abgebildet. Dieses Element von B
schreiben wir als
A wird von
der Funktion f
auf ein Element von B
abgebildet. Dieses Element von B
schreiben wir als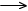 R
R