
Didaktischer Kommentar: Funktionen - Einstieg

 Der Lernpfad "Funktionen - Einstieg"
kann zum Einstieg in das Thema Funktionen in der 5. Klasse AHS (9. Schulstufe)
eingesetzt werden. Anhand konkreter Aufgabenstellungen soll mit Hilfe des Einsatzes
elektronischer Medien Vorwissen aus der Unterstufe aktiviert und vertieft (verschiedene
Darstellungsformen für Funktionen wie Formel, Wertetabelle, Graph) sowie
neue Kenntnisse zum Funktionsbegriff (Präzisierung der Funktionsdefinition,
Bezeichnungen wie Definitionsmenge, Zielmenge, Argument, Funktionswert,…)
erarbeitet und an komplexeren Aufgabenstellungen angewendet werden.
Der Lernpfad "Funktionen - Einstieg"
kann zum Einstieg in das Thema Funktionen in der 5. Klasse AHS (9. Schulstufe)
eingesetzt werden. Anhand konkreter Aufgabenstellungen soll mit Hilfe des Einsatzes
elektronischer Medien Vorwissen aus der Unterstufe aktiviert und vertieft (verschiedene
Darstellungsformen für Funktionen wie Formel, Wertetabelle, Graph) sowie
neue Kenntnisse zum Funktionsbegriff (Präzisierung der Funktionsdefinition,
Bezeichnungen wie Definitionsmenge, Zielmenge, Argument, Funktionswert,…)
erarbeitet und an komplexeren Aufgabenstellungen angewendet werden.
| Kurzinformation | |
|---|---|
| Schulstufe | 5. Klasse AHS (9. Schulstufe) |
| Dauer | ca. 6 UE (mehr bei geringen Vorkenntnissen der Schüler/innen in der Handhabung des elektronischen Werkzeugs) |
| Verwendete Medien | CAS, Derive, Excel, Applets, Animationen |
| Technische Voraussetzungen | Flash, Java, Web-Anbindung |
| AutorInnen | Irma Bierbaumer, Franz Embacher, Helmut Heugl |
Allgemeinbegriffe erwirbt man in der Regel durch die Erfahrung und Begegnung mit prototypischen Repräsentanten (den Begriff "Tisch" verinnerlicht man nicht, indem man eine exakte Definition gibt, sondern weil man verschiedene Prototypen des Tisches erlebt). So verinnerlichen Lernende die fundamentale Idee der Funktion auch nicht durch eine "saubere" Definition am Beginn des Lernprozesses, sondern indem er verschiedene Prototypen dieses Begriffes möglichst anhand von Beispielen aus seiner Erfahrungswelt erlebt [Dörfler, 1991].
Im Laufe des "Funktionenlernens" erleben Lernende verschieden Prototypen des Funktionsbegriffes:
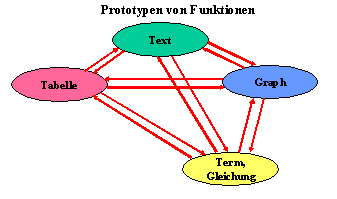
"Funktionenlernen" besteht im Wesentlichen darin, einen Prototypen zu finden, Beziehungen zwischen Prototypen herzustellen oder bestimmte Prototypen für das Problemlösen zu nutzen.
Text <-> Tabelle <->Formel (=Funktionsgleichung) <->Tabelle <-> Graf |
|
| Handybeispiel (1) | Aus einem Text eine Tabelle, eine Gleichung finden. |
| Handybeispiel (2) | Mit einem geeigneten elektronischen Werkzeug eine Tabelle erstellen. |
| Handybeispiel (3) | Die Tabelle zum Problemlösen nutzen. |
| Schachtelbeispiel (1) | Aus einem Text, einer Skizze, einer Flashanimation eine Formel (Funktionsgleichung) finden. |
| Schachtelbeispiel (2) | Aus einer Formel eine Tabelle mit variabler Schrittweite erstellen. |
| Handybeispiel (4) und Schachtelbeispiel (3) | Aus dem Text bzw. der Funktionsgleichung Eigenschaften der jeweiligen Funktionen ableiten können. |
| Schachtelbeispiel (5), Handybeispiel (4) und (5) | Aus Gleichungen und Tabellen Graphen mit Hilfe geeigneter elektronischer Werkzeuge ermitteln können. |
In allen Schularten ist die Nutzung von informationstechnologischen Medien verpflichtend vorgeschrieben.
Allgemein bildende höhere Schule (AHS)
5. Klasse
Funktionen
- Beschreiben von Abhängigkeiten, die durch reelle Funktionen in einer Variablen erfassbar sind (mittels Termen, Tabellen und Graphen), Reflektieren über den Modellcharakter von Funktionen
- Beschreiben und Untersuchen von linearen und einfachen nichtlinearen Funktionen
- Untersuchen von Formeln im Hinblick auf funktionale Aspekte, Beschreiben von direkten und indirekten Proportionalitäten mit Hilfe von Funktionen
- Arbeiten mit Funktionen in anwendungsorientierten Bereichen
Höhere technische und gewerbliche Lehranstalten (HTL)
1. Jahrgang
Funktionen
- Begriff, Darstellung im Koordinatensystem; lineare Funktion; Interpretieren von Tabellen, …
Handelsakademien (HAK)
II. Jahrgang
Funktionen, Umkehrfunktionen, …
Höhere Lehranstalten für wirtschaftliche Berufe (HLW)
Lehrplan ist nicht jahrgangsbezogen
Funktionenlehre
- Lineare Funktionen und dazugehörige Gleichungen
- Potenz- und Wurzelfunktionen, …
- Anwendungsbeispiele und Projekte zu funktionalen Zusammenhängen
Bildungsanstalt für Kindergartenpädagogik (BAKIP)
2. Klasse
Funktionen
- Lineare Funktionen, Potenzfunktionen, Wurzelfunktionen
Dörfler, Willi. (1991): "Der Computer als kognitives Werkzeug und kognitives Medium" in Computer - Mensch - Mathematik. Verlag Hölder-Pichler-Tempsky, Wien, 1991, S. 51. ISBN3-209-01452-3.