| Station 16 | Verhalten im Unendlichen | J | G |
|
Aufgabe 1 Kannst du den Funktionsgraphen die richtigen Funktionsterme zuordnen? |
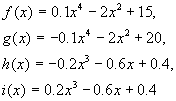 |
| Bild 1 | Bild 2 | Bild 3 | Bild 4 |
Bei der Zuordnung der Funktionen solltest du dir zunächst überlegen, welchen Grad die Funktionen haben könnten..
Weißt du noch, woran man am Graphen den Grad einer Funktion erkennen ( oder vermuten) kann ?
Beschreibe den Verlauf der Graphen . Verwende dazu Ausdrucksweisen wie "von links unten nach rechts oben" oder "von links oben nach rechts unten" .
Bei ganzrationalen Funktionen kann man direkt am Funktionsterm ablesen, welchen Verlauf die Graphen haben.. Dabei spielen die Koeffizienten der Polynome eine wichtige Rolle.
Im folgenden Programm kannst du die Koeffizienten des Polynoms verändern. Überlege dir bei der Betrachtung des Funktionsverlaufs, in welche Richtung (nach oben oder unten) der Graph verläuft, wenn man für x sehr große positive Werte (z.B. 1000000) oder betragsmäßig hohe negative Werte ( z.B. -20000000) einsetzt.
|
Du kannst die
Koeffizienten Untersuche,
welcher Summand Versuche, eine
Funktion zu erzeugen, die von links unten Erzeuge nun
eine Funktion, die |
Formuliere in deinem Heft einen Satz über den Verlauf von ganzrationalen Funktionen ( in Abhängigkeit von dem Grad der Funktion und ihren Koeffizienten).
Aufgabe 2
Beschreibe den Verlauf der folgenden Funktionen für betragsmäßig große x-Werte.
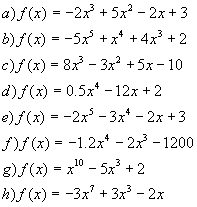
Du kannst deine Ergebnisse
überprüfen, indem du die Funktionen zeichnen lässt
(z. B. mit Derive, TI 89 oder mit dem oben stehenden Programm).
| zurück |

