Wie verläuft die Straße?

1. Skizze

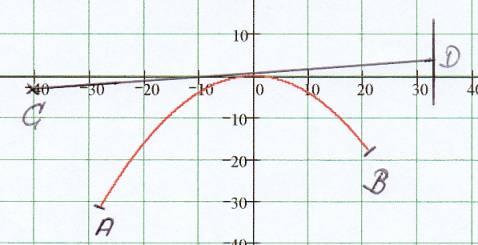
2. Stauchungsfaktor der Parabel bestimmen:
   
   a)       f_a(x) =  a x²  ;  Koordinaten von Punkt A einsetzen liefert  a = -0,04
   
   
3. Steigung zwischen  C  und  D  bzw.  D ´ :
   
   Das Steigungsdreieck bzw. die Steigungsformel liefert 0,07 = 7% für C  und  D  und  0,06 = 6%  für  C  und  D´. Diese Werte sind plausibel, da der y-Wert von D´ kleiner ist als der von  D.
   
   
4. Steigung der Parabel mit der Gleichung y = -0,04x² im Punkt P(x₀ | y₀):
   
   Mit der Steigungsformel für eine Tangente an eine Ursprungsparabel  m = 2 a x₀  erhält man x₀ = -0,875 bzw.
   x₀ = -0,75.
   
   Durch Einsetzen in die Funktionsgleichung erhält man  y₀, also P (-0,875 | -0,031)  bzw.  P´(-0,75 | -0,023).
   
   
5. Man kann durch Einsetzen in die jeweilige Geradengleichung nachweisen, dass C ,  D  und  P  nicht auf einer Geraden liegen und dass das für die Punkte P´ und D´ sehr wohl gilt:
   
   P: 0,07(-0,875) + 0,4275 = 0,36625  (ungleich -0,031)
   P´: 0,06(-0,75) + 0,02 = -0,025 (ungefähr gleich -0,023)