| Station 14 | Lösungen | JJ |
Rote Zahlen bei der Donald AG
1.Die zu untersuchende Gewinnfunktion errechnet sich durch
Gewinn = Einnahmen - Kosten, also g(x) = 10x - k(x) .
Dies ergibt ausgerechnet g(x) = -0,3x³ + 5x² -16x -10.
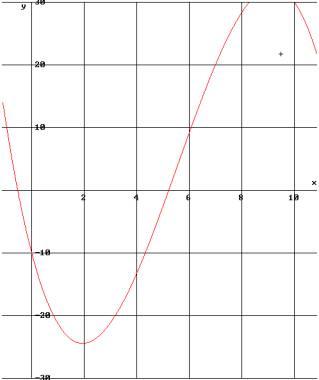
Ein Plot der Funktion zeigt, dass die Firma mehr als 5 Tonnen pro Stunde produzieren müsste, um keine Verluste zu erleiden.
Die Lösung der Gleichung g(x) = 0 liefert den genauen Wert der gesuchten Nullstelle. Erst bei einer Produktion von x » 5,22 Tonnen pro Stunde würde die Firma aus den roten Zahlen kommen. Sie kann jedoch nur höchstens 5 Tonnen produzieren. Der optimale Produktionswert liegt bei x = 5. Allerdings macht die Firma wegen g(5) = -2,5 dabei immer noch Verluste.
2.
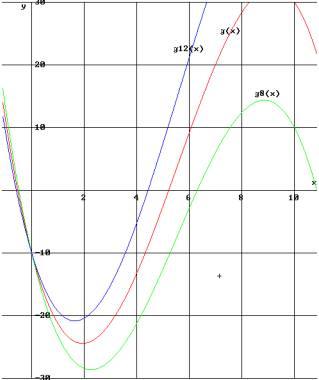
Der Graph von g8(x) = 8x
- k(x) zeigt, dass die Verluste bei einem Preisverfall auf 8 Euro natürlich
noch größer werden.
Dagegen würde ein Preisanstieg auf 12 Euro die Firma in die Gewinnzone bringen, denn g12(x) = 12x - k(x) erreicht bereits bei x » 4,43 den sogenannten Break-even-point, d.h. den Punkt, an dem der Erlös genau die Kosten deckt (g(x)=0) und die Gewinnzone beginnt. Der maximale Gewinn liegt bei einem Preis von 12 Euro bei einer Produktion von 5 Tonnen pro Stunde und beträgt 7,5 Euro.
 |
Zusatz:
Um zu untersuchen, ab welchem Preis die Firma keine Verluste mehr macht,
stellt man die Gleichung p
. 5 - k(5) = 0 auf und löst sie nach p auf. Man erhält den
Marktpreis von 10,5 Euro.
| zurück |
