RSA - Realisierung mit CAS
Inhalt:
- Vorgangsweise - theoretisch
- Vorgangsweise - praktisch (mit DERIVE)
- Vorgangsweise - praktisch (mit MATHEMATICA)
- Anwendung mit maßgeschneiderten Funktionen
Die Realisierung des RSA-Verfahrens mit einem Computeralgebrasystem hat zwei entscheidende Vorteile gegenüber der Realisierung in einer Programmiersprache. Das CAS bringt bereits die nötigen Rechenfertigkeiten im Umgang mit Primzahlen und sehr großen Zahlen mit - der Anwender kann sich also auf den Algorithmus konzentrieren.
Betrachten wir nochmals den Ablauf eines asymmetrischen Verfahrens:
Die ursprüngliche Idee hinter allen asymmetrischen Verschlüsselsverfahren ist die Lösung eines sicheren Schlüsselaustauschs ohne physikalisches Treffen der Kommunikationspartner - also über einen unsicheren Kanal (z.B. über Internet). Dazu dienen Public-Key-Verfahren, bei denen es zwei Schlüssel gibt - einen öffentlichen, der nur zum Chiffrieren (Verschlüsseln) dient, und einen geheimen (privaten), mit dem man die verschlüsselten Nachrichten wieder dechiffrieren (entschlüsseln) kann.
Hinweis: Public-Key-Verfahren - Public Key + Private Key (2 Schlüssel!)
- Public Key = Öffentlicher Schlüssel - für jeden zugänglich, nur zum Chiffrieren / Verschlüsseln!
- Private Key = Geheimer / Privater Schlüssel - zum Entschlüsseln
RSA beruht auf der Tatsache, dass es schwierig (extrem zeitaufwändig) ist, große Zahlen zu faktorisieren. Wir haben hier den Fall einer Einwegfunktion mit Falltür.
Die Funktion lässt sich in eine Richtung leicht berechnen (= verschlüsseln mit Public Key), die Umkehrung ist allerdings sehr aufwändig (knacken der verschlüsselten Information) - es sei denn, man hat eine Falltür / Zusatzinformation (= Private Key) zur Verfügung.
Vorgehensweise - theoretisch:
- Man wählt zwei (sehr große) Primzahlen p und q, von denen im öffentlichen Schlüssel das Produkt
n = p . q bekannt gegeben wird. - Anschließend konstruiert man zwei spezielle Exponenten, einen "öffentlichen" a und einen "privaten" b, die bestimmte Bedingungen erfüllen müssen.
- a muss zu m = (p-1)(q-1) teilerfremd sein: a mod m = 1
- b = a-1 mod m (modulare Inverse - Berechnung mittels Erweitertem euklidischen Algorithmus)
- "Witz" dabei: b lässt sich aus a nicht berechnen, ohne die Primzahlen p und q zu kennen.
Mit der Kenntnis von n (Produkt der beiden Primzahlen p und q) und dem öffentlichen Schlüssel a kann nun mit folgender Formel eine Nachricht x verschlüsselt werden. - Nur, wer den Privaten Schlüssel b kennt, kann die geheime Information auch wieder entschlüsseln. Dies funktioniert laut Satz von Euler nach folgender Formel:
Klartext x = yb mod n
Geheiminformation y = xa mod n
Der Algorithmus ist solange sicher, solange die zugrundeliegenden Primzahlen (Schlüssellänge) groß genug gewählt werden und niemand eine schnelle Möglichkeit zur Faktorisierung findet.
Tipp: Die beiden Primzahlen p und q und das Produkt m sollten aus Sicherheitsgründen nach der Ermittlung von n und den beiden Schlüsseln vernichtet werden!
Vorgehensweise - praktisch (mit DERIVE):
Verschlüsselung:
Wir wählen zwei Primzahlen p und q - das CAS unterstützt uns dabei mit dem Befehlen PRIME?(z) und NEXT_PRIME(z) bzw. PREVIOUS_PRIME(z) - der Überprüfung, ob eine Zahl z eine Primzahl ist bzw. der Berechnung der zur eingegebenen natürlichen Zahl z nächstgelegenen Primzahl größer z (NEXT) oder kleiner z (PREVIOUS).
Anschließend erzeugen wird die Produkte n = p . q und m = (p - 1) (q - 1)

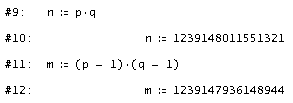
Wir brauchen neben n noch den zweiten Teil des öffentlichen Schlüssels, eine Zahl a, die teilerfremd zu m is. Die Überprüfung geht über die Frage: ist der größte gemeinsame Teiler gleich 1 -->
Wir wählen eine beliebige Zahl, erzeugen die nächstgelegene Primzahl und überprüfen den GGT.

Damit ist mit den beiden Zahlen n und a der öffentliche Schlüssel fertiggestellt.
Die Verschlüsselung kann damit über die Formel
y = xa mod n
erfolgen.
Wir verschlüsseln den Text "KRYPTOGRAFIE" - dazu wandeln wir die Buchstaben in Zahlen um und verwenden dafür den international üblichen ASCII-Code. Wir fassen jeweils 6 Buchstaben zu einer Gruppe zusammen und erhalten 12-stellige Zahlen.
| K | R | Y | P | T | O |
|---|---|---|---|---|---|
| 75 | 82 | 89 | 80 | 84 | 79 |
| G | R | A | F | I | E |
| 71 | 82 | 65 | 70 | 73 | 69 |
Wir verwenden den DERIVE-Befehl: POWER_MOD(x,a,n) - Resultat von xa mod n.
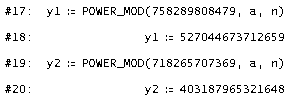
Entschlüsselung:
Zuerst brauchen wir den geheimen Schlüssel - passend zum öffentlichen Schlüssel a, n.
Wir wählen den geheimen Schlüssel b so, dass das Produkt a . b kongruent 1 bezüglich des Modulus m ist. Dies ist gleichbedeutend mit b = a-1 mod m. Dafür verwenden wir den Befehl INVERSE_MOD(x,a).

Anschließend kann die Entschlüsselung durchgeführt werden - analog zur Verschlüsselung, aber mit Hilfe des geheimen Schlüssels!
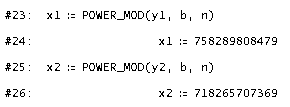
Die Entschlüsselung ergibt wieder die ASCII-Codes der Buchstaben von "KRYPTOGRAFIE" (wie bei der Verschlüsselung in 6-er-Blöcken geordnet).
Vorgangsweise - praktisch (mit MATHEMATICA):
Die Vorgehensweise ist analog zu DERIVE. Es ändern sich nur die Namen der Befehle und ihre Schreibweise. Achtung: einige der Befehle zu Primzahlen sind erst ab der Mathematikca-Version 5.2. im "Standard-Wortschatz" enthalten. Bei den Vorversionen muss das Paket vorher geladen werden.
Befehle:
- PrimeQ[z] ... überprüft eine Zahl z, ob es sich um eine Primzahl handelt
- NextPrime[z], PreviousPrime[z] ... bestimmt die zu z nächstgelegene Primzahl größer bzw. kleiner z
- PowerMod[x, a, n] ... Resultat von x^a mod n
- PowerMod[a, -1, m] ... Berechnung der Modularen Inversen von a (b = a^(-1) mod m)
Anwendung mit maßgeschneiderten Funktionen
Die Probleme bei DERIVE liegen nicht in der Berechnung, sondern dort, wo die Stärken einer maßgeschneiderten Softwarelösung liegen:
- der Verbindung zu Textelementen
- der bequemen Ein- und Ausgabe
- Export / Import ...
Hinweis: Da die Berechnung natürlich im Zahlenbereich erfolgt, die Eingabe aber meist in Textform vorliegt, müssen diese zuerst in Zahlen umgewandelt werden (die einfachste Methode führt über den ASCII-Code). Da die Texte nach der Umwandlung oft länger sind als das Produkt der ursprünglich gewählten Primzahlen, muss zusätzlich noch eine Zerlegung der Texte in passende Blöcke durchgeführt werden.
Mit einer etwas "aufgebohrten" Version unserer vorherigen Berechnung lässt sich die Funktionsweise aber auch mit DERIVE recht gut zeigen.
| Funktion | Erklärung |
|---|---|
| rsa_code(Klartext, Modul, öff. Hochzahl) | Chiffrierung eines im ASCII-Format vorliegende Textes (in DERIVE mit Hochkomma kennzeichnen). Ergebnis ist ein Vektor mit Zahlen. |
| rsa_decode(Geheimtext, Modul, Geh. Hochzahl) | Dechiffrierung eines Zahlenvektors - Ergebnis ist ASCII-Code. |
- DERIVE-Datei - Funktionen rsa_code und rsa_decode
- DERIVE-Datei - Funktionen rsa_code und rsa_decode mit einem Übungsbeispiel
© letzte Änderung am 29. Oktober 2005