| Du möchtest ... |
Du gibst ein ... |
| ... bereits erzeugten Audruck oder Teilausdruck
kopieren, um ihn in die Eingabezeile einzutragen |
Kursor an die betreffenden Stelle in der
Eingabezeile (s.o.) bewegen, dann den zu kopierenden Ausdruck markieren,
mit F3 wird das Markierte dorthin kopiert, wo der Cursur im
Eingabefeld steht. |
|
... z.B. die Matrix  eingeben eingeben
|
Schreiben-> Matrix oder  anklicken. Nach der Eingabe der gewünschten Anzahl von Zeilen
und Spalten öffnet sich eine Dialogbox zum Eingeben und Bearbeiten
der gewünschten Ausdrücke
anklicken. Nach der Eingabe der gewünschten Anzahl von Zeilen
und Spalten öffnet sich eine Dialogbox zum Eingeben und Bearbeiten
der gewünschten Ausdrücke
oder ...
direkt im Eingabefeld  eingeben
(Achtung Zeilenende mit Semikolon!) eingeben
(Achtung Zeilenende mit Semikolon!)
|
| ... der eingegebenen Matrix den Namen A
zuweisen |
in die Eingabezeile eingeben A : =
|
... die 3x1-Matrix (den Vektor) 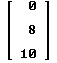 eingeben eingeben |
Schreiben-> Vektor; Angabe der
Anzahl der Komponenten; dann Eingabe
oder direkt ins Eingabefeld als  (Semikolon
beachten!) (Semikolon
beachten!) |
| ... Matrizen A und B verknüpfen z.B.
durch Adddition zum Ergebnis C |
In die Eingabezeile mit F3 markierte Matrizen A + B
eingeben
|
| ... die Matrix A transponieren |
Eingabe A`
|
| ... die inverse Matrix berechnen |
A^(-1)
|
... das LGS 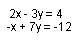 lösen
lösen |
Mit der ROW_REDUCE (A,B) :
A ist dabei die Koeffizientenmatrix, B die einspaltige Matrix auf
der rechten Seite des LGS A * X = B |
... das LGS 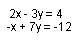 lösen
lösen |
Lösen -> Gleichungsystem, Zahl der Gleichungen angeben,
Koeffizienten in die Matrix eintragen
oder ...
direkt über die Eingabezeile z.B.
SOLVE( [[2x-3y=4, -x+7y=-12], [x,y] )
|
... die Einheitsmatrix 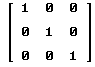 eingeben eingeben |
in die Eingabezeile IDENTITY_MATRIX(3) |
| ...auf das Element a23 einer Matrix M zugreifen |
in die Eingabezeile ELEMENT(M, 2, 3)
|
| ...spezielle Eingabebesonderheiten für
Punkte, Punktemengen, Abbildungen wissen |
|