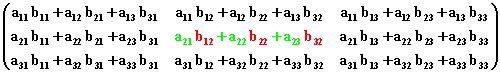Ist A eine (m,n)-Matrix und B eine (n,p)-Matrix, dann heißt die (m,p)-Matrix C das Produkt der Matrizen A und B genau dann, wenn für die Elemente der Matrix C gilt:
cij = ai1 . b1j + ai2 .
b2j + . . . . . + ain . bpj mit 1 
i
m und 1
j
p
Man beachte, dass das Produkt zweier Matrizen nur dann erklärt ist, wenn die linke Matrix ebenso viele Spalten hat, wie die rechte Matrix Zeilen.
Die Matrizenmultiplikation ist keine kommutative Verknüpfung,
d.h. es gilt im allgemeinen nicht 
Die Matrizenmultiplikation ist assoziativ, d.h.
Für den Fall zweier (3,3)-Matrizen wird die Produktmatrix so berechnet :
=
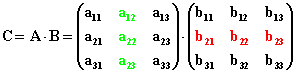