SelMa_Matrixprojekt: Geometrie_elementare Abbildungen-Kurzerläuterung

Hier wollen wir den Weg andersherum gehen und sehen, wie man die in der Aufgabe vorgegebene Abbildungmatrix finden kann, wenn man die Art der Abbildung kennt. Diese hast du mittlerweile sicher gefunden! Wie kann man diese Matrix herleiten? Die folgenden Schritte sollen helfen, auf die Besonderheiten zu achten, die in einem Spezialfall (m=2) zur gesuchten, konkrten Abbildungsmatrix führen. Hast du im Spezialfall die Matrix A gefunden, lässt sich die Herleitung sicher auf den allgemeinen Fall m beliebig übertragen. 1. Gesucht ist also eine Abbildungsmatrix A der Gestalt . 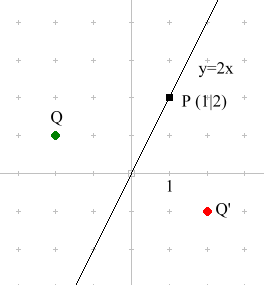Die Matrixelemente a, b, c und d müssen passend bestimmt werden, wie- ist oben klar, a muss z.b. sein!
2. Wir untersuchen Punkt und Bildpunkte bei einer Spiegelung an der Geraden y= 2x. Wie werden Punkte, die auf der Spiegelachse liegen, abgebildet, insbesondere der Punkt P (1\|2)? Drüberfahren über das blau umrahmte Feld ergibt die Antwort! Wie lauten die Bildpunkte des entsprechenden Bildpunktes Q(-2\|1)? Drüberfahren über das blau umrahmte Feld ergibt die Antwort! Wie lautet dann die Matrizengleichung, mit der ich für diese Abbildung typische Bildpunkte aus den vorgegebenen Punkten P und Q bestimmen kann? Drüberfahren über das blau umrahmte Feld ergibt die Antwort!
3. Löse die vorgegebene Matrizengleichung selber! Es ergibt sich wie im folgenden Derive-Protokoll :
Vergleiche mit der vorgegebenen Abbildungsmatrix im hier gewählten konkreten Fall m=2! 4. Auf dieselbe Art kannst du die Abbildungsgleichung für eine Spiegelung an der Geraden y= mx erstellen. Führe wie im Derive-Protokoll die Schritte 1-8 durch und übergebe ggf. die Gleichung 8 zur Lösung an Derive!