|
Das Gauß-Verfahren, benannt nach dem deutschen Mathematiker
und Astronom Carl-Friedrich Gauß (1777-1855), ist ein Verfahren
zur Lösung linearer Gleichungssysteme der Gestalt:
Am Beispiel: Dafür schreiben wir dieses System in folgendes Schema um:
Dieses System wird durch Äquivalenzumformungen zunächst auf "Stufenform" gebracht. Äquivalenzumformungen sind: - Multiplikation oder Division einer Zeile mit/durch eine Zahl. - Addition oder Subtraktion einer Zeile zu/von einer anderen Zeile. Die "Stufenform" beim Gauß-Verfahrens bedeutet, dass zunächst in der 1.Spalte unterhalb des 1.Elementes durch geeignete Äquivalenzumformungen der Zeilen schrittweise an allen Stellen eine Null erzeugt wird. Danach erhalten wir das Schema: Dies wird bei (grösseren Systemen) analog mit den weiteren Spalten solange wiederholt, bis unterhalb einer Diagonalen nur noch Nullen stehen: Nun können wir, falls in der Diagonale keine Nullen stehen, von unten nach oben arbeitend durch entsprechende Äquivalenzumformungen an allen Stellen oberhalb der Diagonalen eine Null erzeugen. Endergebnis der Umformungsschritte: d.h es gilt also, wie man leicht durch Nachrechnen feststellt:
|
 werden
wir das Gauß-Verfahren in einigen Schritten kennenlernen.
werden
wir das Gauß-Verfahren in einigen Schritten kennenlernen.
 Nun
verfährt man in der 2.Spalte unterhalb des 2.Elementes genau so.
Nun
verfährt man in der 2.Spalte unterhalb des 2.Elementes genau so.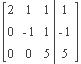
 In
der rechten Spalte des Schemas steht nun der Lösungsvektor
In
der rechten Spalte des Schemas steht nun der Lösungsvektor 
