Zur MathePrisma-Startseite
Zur Modul-Startseite  


Diskrete Verteilung (Geometrische Verteilung 1 )
 

  
 
  
Stellen Sie sich vor, J.W. steht wie am Ende des letzten Kapitels beschrieben nachts vor seiner Haustür.
Jetzt geht er aber nach einer anderen Methode vor. Er probiert einen Schlüssel, und wenn dieser nicht passt, schüttelt er den Schlüsselbund und probiert es von neuem mit irgendeinem der zehn Schlüssel.
 
  
Wie groß ist nun mit dieser Methode die Wahrscheinlichkeit, dass J.W. genau sechs Versuche braucht, um den passenden Schlüssel zu finden?
Bitte geben Sie wieder das Ergebnis als Dezimalzahl mit zwei Nachkommastellen Genauigkeit an!
Die Wahrscheinlichkeit ist jetzt: 
Falls Sie die hier gesuchte Wahrscheinlichkeit nicht berechnen können, sollte Sie das nicht entmutigen, denn hier ist eine neue (allerdings nicht zu schwierige) Überlegung von Ihnen gefordert.
 
  
Um genau beim 6. Versuch erfolgreich zu sein, müssen die ersten fünf Versuche erfolglos und der sechste Versuch erfolgreich sein.

Die Wahrscheinlichkeit dafür ist:


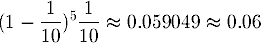
Man beachte, dass hier kein Binomialkoeffizient auftaucht. Es gibt nämlich nur eine einzige Möglichkeit dafür, genau beim sechsten Versuch erstmals erfolgreich zu sein.
 
  
geometrisch
verteilt
 Allgemein berechnet man die Wahrscheinlichkeit dafür, dass sich bei einer Folge von nacheinander durchgeführten Bernoulli-Versuchen genau beim k-ten Versuch zum ersten Mal ein "Erfolg" einstellt (die vorhergehenden Versuche sind dann "Misserfolge") mit:

 
  
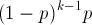
Seite 8/14