| |
| |
|
Um die Flugbahn zu berechnen, ist es sinnvoll, zunächst die Horizontal- und Vertikalbewegung getrennt zu betrachten:
|
| |
 horizontale Flugbewegung |
Die Horizontalbewegung ist unbeschleunigt.
|
| |
|
Damit können wir bereits die Bewegung des Pakets in horizontaler Richtung beschreiben:
|
| |
unbeschleunigte Bewegung
|
Satz (Beschreibung unbeschleunigter Bewegungen)
Bewegt sich ein Körper entlang einer geraden Bahn mit konstanter Geschwindigkeit v, so ist die zurückgelegte Strecke s proportional zur verstrichenen Zeit t. Es gilt also:
|
| |
|
Du kannst Dir das im Folgenden veranschaulichen:
|
| |
 konstante Geschwindigkeit |
|
| |
|
Zum anderen fliegt das Paket aber auch nach unten, und zwar mit zunehmender Zeit immer schneller:
|
| |
vertikale Flugbewegung |
Die Vertikalbewegung ist gleichmäßig beschleunigt
|
| |
|
Auch eine solche gleichmäßig beschleunigte Bewegung lässt sich durch eine Funktion beschreiben:
|
| |
beschleunigte Bewegung
|
Satz (Fallgesetz der Physik: Beschreibung gleichmäßig beschleunigter Bewegungen)
Lässt man den Luftwiderstand unberücksichtigt, so fallen alle Gegenstände mit derselben Beschleunigung, der sogenannten Erdbeschleunigung, zu Boden. Für die zurückgelegte Strecke s ergibt sich somit folgender Zusammenhang:
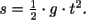Dabei bezeichnet g die experimentell bestimmte Erdbeschleunigung. Es gilt:
|
| |
|
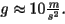
Es war Galileo Galilei (1564 - 1642), der diese Hypothese aufstellte und experimentell belegte:
|
| |
Experiment |
|
| |
|
Fügt man nun die Horizontal- und Vertikalbewegung wieder zu einer Gesamtbewegung zusammen, so sieht man, dass die Flugbahn parabelförmig ist:
|
| |
|
|
| |
|
Indem man nun die Horizontal- und Vertikalbewegungen wieder zusammensetzt, erhält man die Funktion der Flugbahn:
|
| |
Beschreibung der Flugbahn durch eine Funktion
|
|
| |
