MathePrisma: Kombinatorik


		Kombinatorik (Kombinatorische Grundaufgaben¹)

Ziehen
MIT
Zurücklegen,
MIT
Beachtung der Reihenfolge
einfaches Urnenexperiment

In einer Urne befinden sich eine gelbe, eine grüne, eine blaue und eine rote Kugel
(also ist n=4).

Sie ziehen eine Kugel aus der Urne (z.B. die rote)
und legen sie wieder zurück.
Danach ziehen Sie ein weiteres Mal eine Kugel.

(also ist k=2, zweimaliges Ziehen)

Nehmen wir an, Sie interessiert nicht nur, welche zwei Kugeln Sie gezogen haben, sondern auch noch, in welcher Reihenfolge Sie die Kugeln gezogen haben.

Es macht also für Sie einen Unterschied, ob Sie z.B. zuerst die rote und dann die blaue Kugel gezogen haben oder ob Sie umgekehrt zuerst die blaue und dann die rote Kugel gezogen haben.

Frage

Wieviel mögliche Ergebnisse hat dieses Urnexperiment?
Falls Sie das nicht direkt beantworten können, können Sie weiter unten auch ohne Stift und Papier das zugehörige Baumdiagramm erstellen (und damit die Anzahl der Möglichkeiten bestimmen).

Hier können Sie das zugehörige Baumdiagramm selbst erstellen!

mit Zurücklegen, mit Beachtung der Reihenfolge
`n=4, k=2`

Klicken Sie zum Erstellen des Baumdiagramms einfach mit der Maus auf die vier verschiedenfarbigen Kugeln. Jeder Klick entspricht einem Zug aus der Urne. Wenn Sie das Baumdiagramm fertig erstellt haben, können Sie auf "Zählen" klicken, um die Anzahl der Möglichkeiten abzulesen.

Bitte scrollen Sie so lange, bis Sie den ganzen rot umrandeten Bereich sehen!

Lösung:

Für die erste Kugelziehung gibt es vier Möglichkeiten: rot, gelb, grün und blau. Da Sie die Kugel aus der ersten Ziehung wieder zurücklegen und Sie die Reihenfolge beachten wollen, gibt es zu jedem der vier möglichen Ergebnisse der ersten Ziehung wieder vier mögliche Ergebnisse für die zweite Ziehung.
Damit gibt es insgesamt 4^.4 = 4² = 16 mögliche Ergebnisse für das Zufallsexperiment "zweimal Ziehen mit Zurücklegen unter Beachtung der Reihenfolge".

Wie sieht die Verallgemeinerung aus ?

Aufgabe: Überlegen Sie sich selbst, wie Sie obige Überlegung auf den allgemeinen Fall der Ziehung von k Kugeln aus einer Urne mit n Kugeln anwenden können!

Verallgemeinerung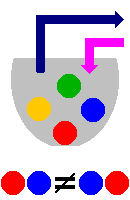

Für die Auswahl ("Ziehung")

von k Elementen ("Kugeln")
aus einer Menge mit n Elementen ("Urne")
mit Wiederholung ("Zurücklegen")
und mit Berücksichtigung der Reihenfolge

gibt es

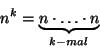
Möglichkeiten.

Falls Sie eine Anwendung dieser Überlegungen sehen möchten, klicken Sie auf Beispiel Fußball-Toto .
Falls nicht, betrachten wir jetzt das Ziehen ohne Zurücklegen, aber immer noch mit Beachtung der Reihenfolge ...

Seite 4/8