Thema: Faktorisieren

Mit Hilfe des Distributivgesetzes haben wir Summen mit einer Zahl bzw. mit einer weiteren Summe multipliziert.

Beispiel: (2a + 4b)∙3c = 6ac + 12bc

Multiplikation einer Summe

===================>

Faktorisieren

<===================

Wann ist diese Umkehrung notwendig?

Wir zerlegen Zähler und Nenner in ein Produkt und können nun einen gemeinsamen Faktor kürzen.

Beispiel: a) = =

b) 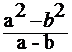= = a+b

Bestimmung einer Lösungsmenge.

Umstellen einer Gleichung!

c) 2x +ax = 5

<=> x·(2 + a) = 5

<=> x =

=======

Methoden des Faktorisierens:

Das musst Du können:

a) Ausklammern:

Bei dieser Methode wird in einer Summe eine Zahl, eine Variable oder gar ein Term gesucht, der in allen Summanden als Faktor enthalten ist. Dieser wird dann „herausgezogen“, d.h. als Faktor mit der Restsumme multipliziert.

Beispiele:

1.) 8a + 4c + 10d = 2·4a + 2·2c + 2·5d = 2·(4a+2c+5d)

Wichtig:

Bei diesem Beispiel wurde nur eine Zahl „ausgeklammert“.

2.) 8ax + 4cx + 10dx = 2x·4a + 2x·2c + 2x·5d = 2x·(4a+2c+5d)

3.) 8ax³ + 4cx² + 10dx = 2x·4ax² + 2x·2cx + 2x·5d = 2x·(4ax+2cx+5d)

4.) 8a(x+y) + 4c(x+y) + 10d(x+y) =

2(x+y)·4a +2(x+y)·2c +2(x+y)·5d = 2(x+y)·(4a+2c+5d)

Bei diesem Beispiel wurde eine Zahl und ein Term (Summe) „ausgeklammert“.

5.) 3ax + 3ay + bx +by = 3ax + 3ay + bx +by= 3a(x+y) + b(x+y)

= 3a(x+y) + b(x+y) = (x+y) (3a+b)

Aufgabe:

Suche in den Fachbüchern selbst nach vergleichbaren Aufgaben!!!

b) Mittels Binomischer Formel

Bei diesem Vorgehen werden die Binomischen Formeln „rückwärts“ ausgewertet!!!!

(a + b)² = a² +2ab +b² Û a² +2ab +b² = (a + b)² … ist doch klar, ODER?

Beispiele:

1.) 9x² +24xy + 16y² = (3x + 4y)² <- 1. Binomische Formel

2.) 36x²y² + 9z² - 36xyz = (6xy – 3z)² <- 2. Binomische Formel

3.) 9x² - b² = (3x-b)(3x+b) <- 3. Binomische Formel

Beachte: Die Reihenfolge muss nicht immer direkt auf die Binomischen Formeln hinweisen. Das musst Du durch sehr viel Übung erkennen. Als erstes Merkmal sind die beiden Quadrate herauszustellen. Anschließend muss die Bedingung „2·a·b“ geprüft werden.

Aufgabe:

Suche in den Fachbüchern selbst nach vergleichbaren Aufgaben!!!

c) gezielte Faktorensuche (Rückgriff auf Satz von Vieta)

Bei dieser Methode wird viel Geschick erwartet und benötig viel Erfahrung im Umgang mit algebraischen Ausdrücken.

Die Idee:

Es gilt: (x+a)(x+b) = x² +bx +ax + ab = x² +(a+b)x +ab

Dann wäre: (x+_)(x+_) = ……………….. =x² + 9 x + 18

Durch Vergleich erhalten wir: a +b = 9 Ù a·b = 18

Die beiden Gleichungen stellen zusammen ein Gleichungssystem dar, das entsprechend gelöst werden kann. Versuche es selbst und erarbeite Dir die entsprechenden Methoden zur Wiederholung.

Vereinfacht können wir wie folgt vorgehen:

18 = a·b = 1· 18 Ù 2· 9 Ù 3· 6

Von dieser Zahlenkombination erfüllt ein Zahlenpaar die erste Bedingung!

3+6 = 9. Folglich muss gelten: x² + 9x +18 = (x+3)(x+6)

Beispiele:

1.) x² + 8x +12 = x² +(2+6)x + 2·6 = (x+2)(x+6)

2.) x² -15x +54 = x² +(-6-9)x +(-6)(-9) = (x-6)(x-9)

3.) x² - 3x -54 = x² +(6-9)x + (+6)(-9) = (x+6)(x-9)

Aufgabe:

Suche in den Fachbüchern selbst nach vergleichbaren Aufgaben!!!