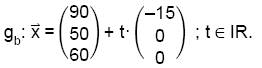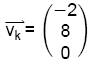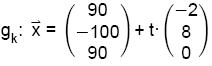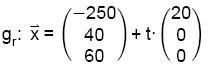In Science-Fiction-Spielen werden Szenen durch Computerprogramme animiert. In einer Mega-City befindet sich eine Straßenkreuzung, die von
Hochhäusern begrenzt wird. Der Verkehr besteht aus fliegenden Raumgleitern, die in klar definierten Flugkorridoren (gestrichelte Linien, s. Abb.2) unterwegs sind.
Zur Vereinfachung werden die Raumgleiter als punktförmig angesehen. |
|
Die x-y-Ebene stellt die Erdoberfläche, die z-Koordinate die Höhe dar. Die in Abb. 2 angegebenen Punkte entsprechen den Eckpunkten des jeweiligen Hausdaches.
Die Dachflächen der Häuser liegen parallel zur x-y-Ebene, die Hauswände stehen senkrecht zur x-y-Ebene. Demnach ergeben sich aus den angegebenen oberen Häusereckpunkten die entsprechenden Fußpunkte der Gebäude mit den
gleichen x- und y-Koordinaten, während die z-Koordinate 0 ist. Die Koordinaten der Punkte sind in Meter, die Zeit ist in Sekunden angegeben.
A.1 In einer Spielsequenz ist Kurt der Pilot eines schwebenden Raumgleiters. Er befindet sich in der Position K (70; −20; 90) und beobachtet die Kreuzung (s. Abb. 2 links und zum Aufgabenende).
3-D-Darstellung mit GeoGebra 5.0
|
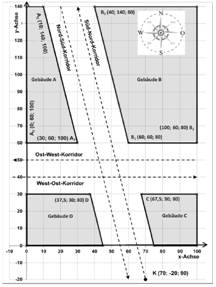
Abb. 2 Draufsicht |
A.1.1 Die Position eines weiteren Raumgleiters ist durch den Punkt R (−330; 780; 190) gegeben. Bestätigen Sie, dass Kurt den Raumgleiter genau über die Hausecke A1 (30; 60; 100) anpeilen kann.
3-D-Darstellung mit GeoGebra 5.0
Zwei Raumgleiter bewegen sich in einer ersten Videosequenz geradlinig mit konstanter Geschwindigkeit. Die Tabelle gibt ihre Positionen zu zwei verschiedenen Zeitpunkten an:
Für die Flugbahn des blauen Raumgleiters ergibt sich damit die Gleichung:
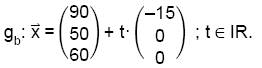
A.1.2 Bestimmen Sie den Schnittpunkt der beiden Flugbahnen und beurteilen Sie, ob Kollisionsgefahr besteht.
3-D-Darstellung mit GeoGebra 5.0
A.1.3 Der blaue Raumgleiter im Ost-West-Korridor wird aus der Sicht von Kurt zunächst durch das Gebäude C verdeckt. Ermitteln Sie den Zeitpunkt, zu dem der blaue Raumgleiter für Kurt
sichtbar wird.
3-D-Darstellung mit GeoGebra 5.0
A.1.4 Die Szene soll durch eine Zentralprojektion mit dem Augpunkt K (70; −20; 90) auf die x-z-Ebene abgebildet werden. Ein Punkt P(x; y; z), y≠ − 20 wird somit auf einen Punkt P‘(x‘; 0; z‘)
in der x-z-Ebene projiziert. Bestimmen Sie Gleichungen zur Berechnung von x‘ und z‘.
3-D-Darstellung mit GeoGebra 5.0
A.2 In einer zweiten Videosequenz setzt sich Kurt mit seinem Raumgleiter zum Zeitpunkt t = 10 s von der Position K aus geradlinig mit gleich bleibender Geschwindigkeit in Richtung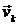 
in Bewegung.
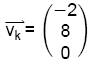
A.2.1 Bestätigen Sie, dass seine Flugbahn mit
 |
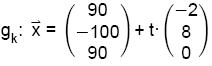; t ≥ 10 beschrieben werden kann. |
3-D-Darstellung mit GeoGebra 5.0
A.2.2 Ein roter Raumgleiter ist zeitgleich mit Kurt losgeflogen und kommt in dessen Blickfeld. Seine Position kann in Abhängigkeit von der Zeit t durch die Gleichung
 |
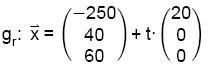; t ≥ 10 beschrieben werden kann. |
Zeigen Sie, dass der Abstand d beider Flugobjekte durch die Funktion
d(t) =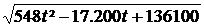 
; t ≥ 10 bestimmt ist.
3-D-Darstellung mit GeoGebra 5.0
Zum Abschluss noch Hilfen zur zweiten Aufgabe der Klausur.
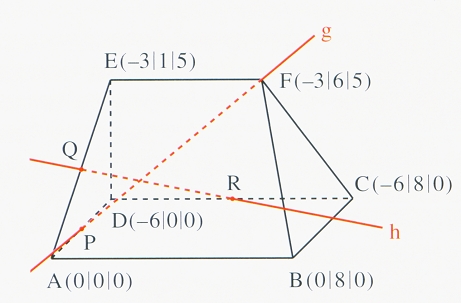
In der dargestellten Figur sind die Punkte P, Q und R die Mitten der jeweiligen Kanten.
3-D-Darstellung der Aufgabe in GeoGebra 5.0
• Stellen Sie die Geradengleichungen in Parameterform auf und belegen Sie Ihre Entscheidung durch eine geeignete Rechnung!
• Schneiden sich die beiden Geraden g (durch P, F) und h (durch Q, R)?
• Stellen Sie die Ebene mit den Punkten B,C und F in der Parameterform und Koordinatenform dar und belegen Sie Ihre Entscheidung durch geeignete Rechnungen!
3-D-Darstellung mit GeoGebra 5.0
• Die Gerade durch die Punkte B und F hat einen Spurpunkt mit der x-z-Ebene. Berechnen Sie die Koordinaten dieses Spurpunktes!
3-D-Darstellung mit GeoGebra 5.0
Download aller GeoGebra-Deiten (zip)
Download aller GeoGebra-Deiten (zi2)
