| Binomialverteilung |
|
Für den beschriebenen Zufallsversuch kann man die Wahrscheinlichkeiten der einzelnen Ereignisse auch berechnen.
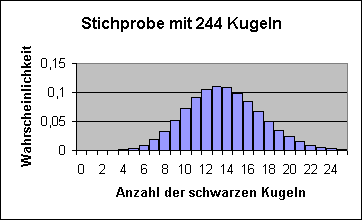 |
Histogramm der berechneten Wahrscheinlichkeiten Beschreibung des Urnenmodells: Es befinden sich 944 weiße und 56 schwarze Kugeln in der Urne. Es soll eine Stichprobe von 244 Kugeln gezogen werden. |
Tabelle der Wahrscheinlichkeitsverteilung
| Anzahl der schwarzen Kugeln | Wahr-scheinlich-keit | Anzahl der schwarzen Kugeln | Wahr-scheinlich-keit | Anzahl der schwarzen Kugeln | Wahr-scheinlich-keit |
|
0
|
7,81928E-07
|
8
|
0,033276474
|
16
|
0,083942407
|
|
1
|
1,13181E-05
|
9
|
0,051763404
|
17
|
0,066785684
|
|
2
|
8,15764E-05
|
10
|
0,072161694
|
18
|
0,04996349
|
|
3
|
0,000390369
|
11
|
0,091063833
|
19
|
0,035255237
|
|
4
|
0,001395237
|
12
|
0,104890616
|
20
|
0,023528389
|
|
5
|
0,003972878
|
13
|
0,111044563
|
21
|
0,01488802
|
|
6
|
0,009387889
|
14
|
0,108691924
|
22
|
0,008952311
|
|
7
|
0,018934895
|
15
|
0,098866666
|
23
|
0,005125973
|
Berechnung der Wahrscheinlichkeit, dass die Anzahl der schwarzen Kugeln in einem bestimmten Intervall [a;b] liegt.
Berechnung der Binomialverteilung
|
|
Berechnungen mit DERIVE |
|
|
Berechnungen mit dem TI 89 |
|
|
Berechnungen mit Excel |
|
|
Darstellung mit DERIVE |
|
|
Darstellung mit dem TI 89 |
|
|
Darstellung mit Excel |