| Station 5 | Gauß'scher
Algorithmus - Vereinfachen von Matrizen - |
|

Carl Friedrich Gauß (1777 - 1855)
ist einer der bedeutendsten
Mathematiker, die je gelebt haben. Von ihm kursiert die Geschichte, dass
er als zehnjähriger Junge in wenigen Augenblicken die Summe der Zahlen
von 1 bis 100 berechnete. Gauß sollte von seinem Lehrer mit dieser
Summierungsaufgabe recht lange beschäftigt werden, er erkannte jedoch
schnell, dass man aus diesen 100 Zahlen 50 Paare bilden kann, die jeweils
einen Wert von 101 haben. Gauß multiplizierte also die Zahlen 50
und 101.
Nach ihm ist der im Folgenden dargestellte Algorithmus
benannt, in dem es um das Lösen von linearen
Gleichungssystemen geht.
Schon im Laufe der Sekundarstufe
I begegnen einem Lineare Gleichungssysteme: zuerst zwei Gleichungen mit
zwei Unbekannten, später drei Gleichungen mit zwei oder drei Unbekannten.
Realistische Probleme,
die durch Lineare Gleichungs- bzw. Ungleichungssysteme dargestellt werden
können, führen in der Regel auf viel größere und
nicht unbedingt quadratische Systeme ( z. B. 52 Gleichungen mit 41 Unbekannten).
Solche Systeme kann man zwar prinzipiell mit den in der Sekundarstufe
I eingeübten Einsetzungs-, Gleichsetzungs- und Additionsverfahren
lösen, doch spätestens bei 4x4 Systemen verrechnet man sich
allzu leicht. Am Besten lässt man den Computer große Gleichungsysteme
lösen. Der muss ein gar nicht mal so schwieriges Rechenschema (eben
den Gauß´schen Algorithmus) mehrfach durchlaufen, bis die
Gleichungen in einer Form dastehen, aus der man leicht die Lösungsmenge
bestimmen kann.
Zur Schreibweise :
Gleichung
I : x1
- 2x2 + 4x3 =
2
Gleichung
II : x1
- x2 + 4x3
= 5
Gleichung III : 2x1
- 3x2 + 9x3 =
12
Man schreibt
man nur die Koeffizienten in eine Matrix:

Subtrahiert man von Zeile II die Zeile I und anschließend das 2-fache
der Zeile I von der Zeile III, so erhält man die beiden folgenden
Matrizen.
 und
und  .
.
Subtrahiert
man nun noch von der Zeile III die Zeile II, erhält man eine Matrix,
aus der man recht leicht die Lösungen bestimmen kann.

Aus
dieser Matrix kann man ablesen, dass für das obige Gleichungssystem
gilt:
x3
= 5 , x2 = 3 und x1 = -12.
Die zweite Matrix ist aus der ersten durch Umformungen hervorgegangen,
die die Lösungsmenge des Systems nicht ändern. Die Frage, welche
Umformungen die Lösungsmenge eines Linearen Gleichungssystems ( LGS
) nicht ändern, ist gar nicht so schwierig zu beantworten.
I :
Man darf Zeilen vertauschen.
( Die Reihenfolge, in der ich die Gleichungen aufschreibe, ist beliebig.)
II
: Man darf Zeilen mit Vielfachen multiplizieren.
( x = 5 oder
25x = 125 sind offenbar äquivalent)
III : Man darf
Zeilen bzw. auch Vielfache von Zeilen addieren.
( Die Bedingungen von zwei Gleichungen
gehen in einer Gleichung
auf. )
Diesen elementaren Umformungen entsprechen die folgenden TI 89 - Befehle:
I :
RowSwap (beispiel,1,3 )
vertauscht die Zeilen I und III der Matrix namens "beispiel"
II
: mRow (4.5,beispiel,2) multipliziert die Zeile II der
Matrix "beispiel" mit 4.5
III : mRowAdd(-3.5,beispiel,1,4)
ersetzt Zeile IV durch -3.5*I + IV
Diese Umformungen gilt es solange auf eine Matrix anzuwenden, bis auf der Diagonalen möglichst nur Einsen stehen und unterhalb der Diagonalen möglichst nur Nullen. Bei größeren Systemen schleichen sich bei vielen Menschen Rechenfehler ein, der Computer langweilt sich auch bei noch so großen Systemen nicht und ist von daher auch das geeignete Instrument für solche eine Rechnung. Trotzdem soll an einem Beispiel, das vom Rechenaufwand her recht freundlich gehaltenen wurde, das Prinzip des Gaußschen Algorithmus verdeutlicht werden.


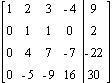


Aus dieser Matrix kann
man ablesen, dass für das obige Gleichungssystem gilt:
x4
=0, x3 = -10 ,x2
= 12 und, x1 = 15
Aufgabe
a)
Welche elementaren
Umformungen
wurden an den Matrizen zwischen den einzelnen "Zuständen"
vorgenommen?
Geben Sie alle elementaren Umformungen in Form von TI-Befehlen ( z.B.
rowswap (m4,1,2) Sto m5 ) an.
Die Zwischenstände werden in den Namen "m1", "m2",
"m3", ... gespeichert. Man kann also jeweils auf den vorherigen
Zustand zurückgreifen, wenn man sich vertippt hat. Nach Beendigung
der Übung sollten Sie nicht vergessen, die Matrizen aus dem Speicher
zu entfernen.
b) Wenden Sie den Gauß´schen Algorithmus auf das folgende in Matrixschreibweise dargestellte Gleichungssytem an:

| zurück |

