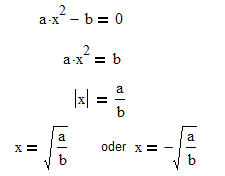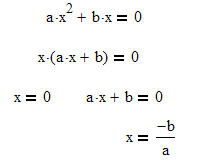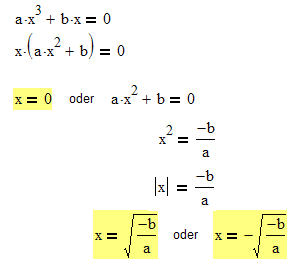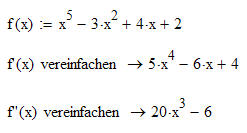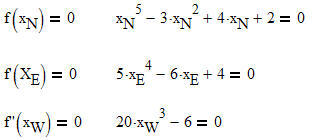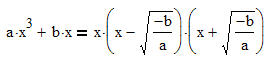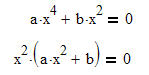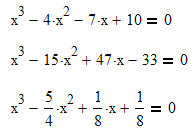Wiederholung:
Um die üblichen Aufgaben der Differential- und Integralrechnung lösen zu können, ist es nicht nur notwendig die Ableitungs- oder Integrationsregeln zu beherrschen, sondern es ist unbedingt notwendig die Grundlagen zum Lösen von Gleichungen jeglicher Art zu absolut sicher zu händeln.
Bruchgleichungen sind immer wieder zu lösen, wenn gebrochenrationale Funktionen untersucht werden.
Quadratische Gleichungen sind im Rahmen der Differentialrechnung zu lösen, wenn die Ableitung einer Funktion zweiten Grades ist.
Üben Sie mit Hilfe von Mathematik.net.
Dort finden Sie auch erklärende Videos.
Übungsaufgaben
Beim Lösen von Gleichungen höheren Grades greifen wie auf das Faktorisieren, auf die Substitution und selbstverständlich auch auf die Lösungsverfahren der quadratischen Gleichungen zurück. Auch die Polynomdivision ist ein ganz wichtiges Hilfsmittel.
Es soll nun versucht werden, die wichtigsten Dinge beispielhaft aufzuzeigen.
A) Die Bruchgleichungen:
... wird bald ergänzt.
B) Die quadratischen Gleichungen
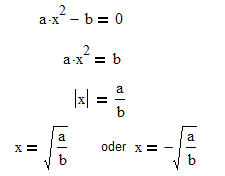 |
Diese Grundgleichung können in den beiden Formen nach Zeile 1 und 2 auftreten
und liefern einfache Lösungen der Form aus Zeile 4. Zu beachten ist die Zeile mit |z|= ...,
denn diese Begründet die Fallunterscheidung und die beiden Lösungen. |
|
Die einfache Form der quadratischen Gleichung sollte nicht mit der quadratischen Ergänzung oder der Lösungsformel gelöst werden.
Merkmal: Die Gleichung hat keinen Linearanteil (c=0). ( ax²+bx+c=0)
Hier wird das Faktorisieren durch ausklammern genutzt, um den Satz vom Nullprodukt nutzen zu können.
Ein Produkt ist immer Null, wenn ein Faktor zu Null wird.
Wichtig ist aber, das wird leider oft vergessen, dass auf einer Gleichungseite ein Produkt und auf der anderen Seite die Null steht. Die Null ist dann auch immer eine Lösung. |
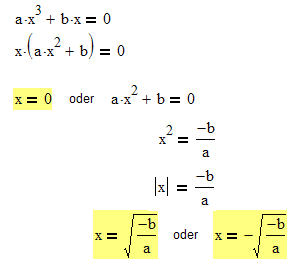 |
Hier sind wir schon bei den Gleichungen höheren Grades. Diese greifen auf die oben genannten Lösungsschritte zurück und sollen daher auch mit gennant werden. |
.... wird bald ergänzt.
C) Die Gleichungen höheren Grades
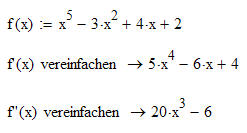 |
Greifen wir als Beispiel eine Funktion 5. Grades auf.
Mit Hilfe der ersten Ableitung können wir die Extremwerte finden.
Mit Hilfe der zweiten Ableitung können wir die Wendepunkte finden und zudem HP und TP unterscheiden. |
Wir haben nun folgenden Gleichungen zu lösen:
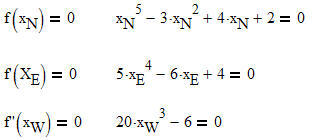 |
In diesem Fall suchen wir die Nullstellen. Zu lösen ist eine Gleichung 5. Grades.
Hier suchen wir die Extremstellen und müssen eine Gleichung 4.Grades lösen.
Hier suchen wir die Wendepunkte und müssen eine Gleichung 3. Grades lösen. |
Die hier genannten Beispiele sind nicht typisch und sollten noch nicht aufgegriffen werden. Klären Sie selbst warum das so ist.
Hier nun die wichtigsten Grundformen für die Gleichungen höheren Grades:
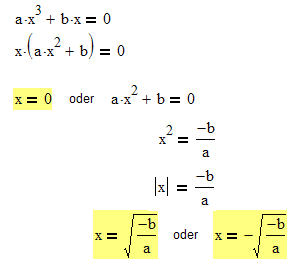 |
Diese Gleichung 3, Grades lässt sich mit Hilfe des Satzes vom Nullprodukt und einer einfachen qaudratischen Gleichung lösen.
Wichtig: Es sollte erkannt werden, dass hier letztlich eine Faktorisierung vorgenommen wird. ax³ +bx wird in Linearfaktoren zerlegt.
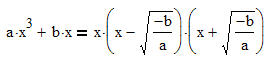
|
|
Auch diese Gleichung 4. Grades lässt sich nach dem obigen Muster lösen.
Die Null ist hier eine "doppelte" Lösung. Für die Differentialrechnung hat diese Tatsache auch eine besondere Bedeutung. Kläre das selbst. |
Bei Gleichungen höheren Grades kann die Substitution weiterhelfen. Das ist immer der Fall, wenn ....... Lesen Sie nach und merken Sie sich die Struktur dieser speziellen Gleichungen.
Ein ganz wichtiges Hilfsmittel ist das Faktorisieren. Hier ist zudem die Polynomdivision ein entscheidendes Instrument.
Prägen Sie sich daher das Muster von Peter Meyer genau ein. -> Musteraufgaben (hier wird noch einmal Schritt für Schritt vorgegangen)
Wer die Vorgehensweise noch einmal selbst am Rechner als interaktive Übung nachvollziehen will, kann das sehr schön mit dem Javascript von Arndt Brünner tun. Wie es geht, zeigt der folgende Film.
Wenn Sie nun bereit sind und glauben eine ausreichende Sicherheit zu haben, prüfen Sie sich und lösen die Übungsaufgaben von Perter Meyer.
Hier nun Gleichungen 3. Grades, die mittels Polynomdivision, Faktorisieren und dem Satz vom Nullprodukt gelöst werden:
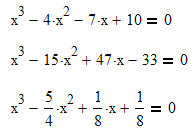 |
Bei diesen Gleichungen ist immer eine ganzzahlige Lösung durch probieren herauszufinden.
Hilfe: Diese ganzzahlige Lösung muss als Faktor im Linearanteil enthalten sein.
Unter Umständen muss diese Gleichung auch erst von den Brüchen "befreit" werden.
Zur ersten Gleichung findest Du hier die Lösung.
Wichtig: Es ist wenig sinnvoll sich erst die Lösung anzusehen und dann es selbst zu versuchen. Mache es umgekehrt!!!!! Das Nachsehen darf erst dann erfolgen, wenn DU es wiederholt versuchst hast, aber keinen Ansatz findest. |
Übungen:
Hier findest Du Übungen mit den Lösungen und Hinweisen für den Lösungsansatz.